Planimetria muflon: Długości boków trapezu prostokątnego tworzą ciąg geometryczny. Ramię, które jest najkrótszym bokiem trapezu ma długość 1. Krótsza podstawa trapezu jest krótsza od drugiego z ramion. Oblicz długość dłuższej podstawy trapezu.

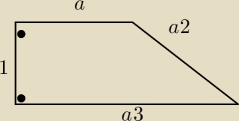
muflon: Tak? 2 i 3 w wykładniku Co dalej?

zawodus: Twierdzenie pitagorasa.

muflon: (a³−a)²+1²=(a²)² Usiłowałem tak, ale nie mogę tego rozwiązać, wychodzi mi tylko a =1, ale to chyba? nie spełnia warunków, bo wtedy któryś bok nie mógłby być najkrótszy.

muflon: uuuup

wredulus: a=q a2=q² a3=q³ Dlaczego Bok 1 takze jest w ciagu geometrycznym stad a=1*q=q

wredulus: U ciebie: a²(a²−1)² = (a²−1)(a²+1) Jako ze a≠1 (warunek ktory wnioskujemy z tresci zadania) To a²(a²−1) = a²+1 Niech b=a² b² − 2b − 1 = 0 .....

zawodus: To nie jedyne rozwiązanie. Jest problem z pojęciem najkrótszy. Wg mnie najkrótszy może być tylko jeden bok, ale z tego co wiem autor dopuszcza takie rozwiązanie.

zawodus: wredulus najlepsze, że "autor" dopuszcza odpowiedź bok =1 czyli twierdzi, że w kwadracie istnieje najkrótszy bok...

wredulus: Dlatego ja wlasnie (ze wzgledu na najkrotszy) dokonalem dzielenia przez a²−1 o czym napisalem

muflon: Właśnie w odpowiedziach jest jedna odpowiedź a=1, co według mnie jest nie logiczne z trescią zadania