Bez sensu 3 bezendu: W prostokącie ABCD , w którym stosunek długości boków AB i BC jest równy 4:3, poprowadzono dwusieczne kątów ADB i BDC . Dwusieczne te przecinają boki AB i CB odpowiednio w punktach K i M . Oblicz stosunek pola prostokąta ABCD do pola trójkąta DKM . Jak to ruszyć ?

Mila: Podpowiedź. Rysunek. x− wspólna miara AB=4x BC=3x BD=5x Tw. o dwusiecznej, potem pola odciętych naroży,..

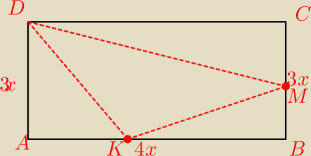
bezendu: A po co mi BD ?

Mila:

	3x		5x
1)		=		i e+f=4x
	e		f

Dalej sam.

bezendu: Ja już ogłaszam kapitulację co do planimetrii

Eta:

Eta: "kapitulacja" III Rzeszy była w maju i Twoja też będzie po10 maja

bezendu: Chyba jednak wcześniej. Bo nic nie mogę pojąć.

Eta: eeeEta..m

bezendu: Etam mi nie pomoże 9 maja. Tam każdy musi liczyć na siebie

Eta: 9 maja Dzień Zwycięstwa !

bezendu: Zobaczymy Oby tak było..

Mila: ?

bezendu: Dziękuję ale wolę zając się bryłami i innymi zadaniami.

bezendu: Jednak spróbuję dokończyć to zadanie. Tylko jak ?

Eta: To łatwe zadanie dokończ

Mila: 23:54 masz proporcję i równanie , oblicz e i f, potem masz już pole ΔAKD. Nad przekątnę stosujesz znowu tw. o dwusiecznej i tak samo liczysz p i q.

bezendu: Ale czemu ja mam obliczać przekątną ?

Mila: Przekątna jest ramieniem kątów , które dzielisz dwusieczną. Rozważasz dwa Δ ΔDAB i ΔDBC

bezendu: Za trudne jak dla mnie.

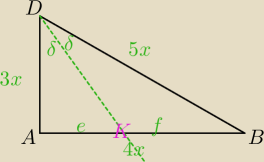
Mila: DK− dwusieczna |AB|=4x Oblicz AK i KB.

bezendu:

3x		5x
	=
4x−y		4x

12x²=20x²−5xy −5xy=−8x² 5y=8x

	8
y=		x
	5

	8
e=		x
	5

bezendu: ?

Eta:

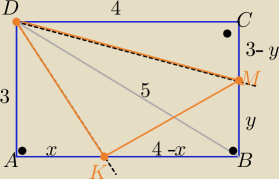
	3		5
z tw. o dwusiecznej :		=		⇒ x=|AK|= ... |KB|=...
	x		4−x

	5		4
		=		⇒ y= ....
	y		3−y

P(ABCD)=12 P(KMD) = P(ABCD)−(P(AKD)+P(KBM)+P(MCD) ) =.... dokończ i nie marudź

Mila: Z Tw. o dwusiecznej.

3x		5x
	=
e		f

3x*f=5x*e 3f=5e e+f=4x e=4x−f 3f=5*(4x−f) 3f=20x−5f 8f=20x

	20
f=		x
	8

	5
f=		x
	2

e=4x−2,5x=1,5x

Eta: @Mila Mamy do wyznaczenia stosunek pól więc śmiało możemy przyjąć wymiary :3,4,5(bez x)

bezendu: dziękuję w końcu zrozumiałem jakieś zadania z planimetrii..

Eta:

bezendu: Jakiś cud chyba w moim wydaniu

Mila:

bezendu: jest jeszcze sens próbować to pojąć ?

Mila: Nie masz wyjścia, musisz .

bezendu: Ale widać co z tego wychodzi ? Niestety. Teraz i tak już nie chodzę do szkoły to od rana do wieczora będę coś próbował.

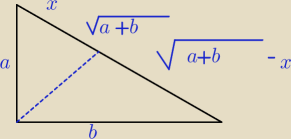
Mila: Znaleźć długość odcinka dwusiecznej kąta prostego w trójkącie prostokątnym o przyprostokątnych a i b.

bezendu:

a		b
	=
x		√a+b−x

	a√a+b
x=
	a+b

	b√a+b
y=
	a+b

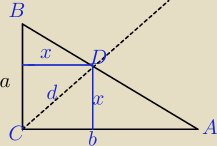
Mila: No, błąd .Przeciwprostokątna? Idź inna drogą. Zauważ, że masz tam kwadrat, (?) Szukasz długości przekątnej. Odcięte Δ są podobne do ΔABC .

bezendu: No a co złego w mym rozumowaniu ?

Mila: Przede wszystkim c=√a²+b², jeśli obliczysz jak została podzielona przeciwprostokątna , to jak obliczysz długość dwusiecznej?

bezendu: No nie wiem właśnie jak obliczyć ? Trzeba z podobieństwa ?

Mila: Sposobów masz kilka. 1) Możesz obliczyć pole ΔABC na dwa sposoby i porównać :

1
	a*b= pole kwadratu +pole Δgórnego+ pole Δbocznego i obliczasz x, d=a√x
2

2) Δboczny ∼ΔABC i obliczasz x 3) 4)

bezendu: Boże, nie wiem jak z tego podobieństwa ? d=√a²+x² ?

Piotr 10: Przepraszam,. ze wchodzę ale mam pytanie Mila dałoby radę z tw o dlugosci dwusiecznej? ''W kazdym trojkacie iloczyn dwoch bokow jest rowny kwadratowi dwusiecznej kata miedzy nimi zawartego powieszkonej o iloczyn odcinkow na ktore ta dwusieczna podzielila trzeci bok' Skorzystanie z tego twierdzenia + skorzystanie z tw o dwusiecznej kata + tw. kosinusów ?

Mila: Można, jeśli to pamietasz, ale trzeba obliczyć na jakie odcinki została podzielona przeciwprostokątna. Może zapisz całe rozwiązanie, to ktoś skorzysta, potem porównamy stopień komplikacji.

Piotr 10: Ok, to jutro zamieszczę rozwiązanie. Głownie tutaj będą komplikacje wyliczenia jednej długości na ktore zostala podzielona przeciwprostokątna( sporo liczenia chyba).

bezendu: ?

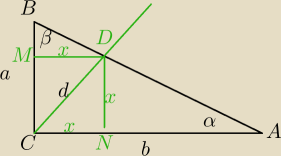
Mila: ΔDNA∼ΔBCA ⇔

x		a
	=		⇔
NA		b

x		a
	=
b−x		b

x*b=a*(b−x) x*b=a*b−a*x ax+bx=ab x(a+b)=a*b)

	a*b
x=
	a+b

	ab√2
d=
	a+b

=================== Proszę rozwiązać z podobieństawa ΔBMD i ΔABC. Zapisz wszystkie obliczenia, oznaczenia jak na rys. w tym wątku.

Mila: Piotrze możesz skorzystać z zależności:

	c*a		c*b
BD=		i AD=
	a+b		a+b

Piotr 10: Tak, widzę już, no to teraz to już po zadaniu . c=√a²+b²( nawet z c 'zejdzie pierwiastek' bo mamy c² ), odpowiednio teraz przekształcić i tyle

bezendu: ΔBMD∼ΔABC

x		BM
	=
b		a

x		a−x
	=
b		a

ax=ba−bx ax+bx=ba x(a+b)=ba

	ba
x=
	a+b

Mila: Dobrze . Skoro nie lubisz podobieństwa to alternatywnie rozwiąż z równoważności pól.

bezendu: Dobrze, ale i tak muszę się tego podobieństwa jakoś nauczyć. Wiem, że jak mi napiszesz co mam robić to zrobię ale sam to nie bardzo.

Mila: Jutro dam parę zadań, może zaskoczysz. Trzeba brać 2 odcinki z jednego Δ i dobrać odpowiadające z drugiego Δ. W końcu to zrozumiesz. W niektórych zadaniach dobrze to już robisz.

bezendu: Wiem, że tak trzeba, ale ja po prostu jak mam tylko wierzchołki to nie wiem jakie dawać oznaczenia bo potem boję się, że mi się nie skróci i w wyniku dostanę coś czego nie miałem w poleceniu.

Mila: Czekam na rozwiązanie, bo zaraz idę spać.

bezendu: Jutro dokończę. Dobranoc.

Mila: DObranoc

bezendu: Nie zapisuje obliczeń ale wyszło tak sam.