jedn Radek: Wyznacz współrzędne środka jednokładności, w której obrazem okręgu o równaniu (x−16)² + y² = 4 jest okrąg o równaniu (x−6)²+(y−4)² =16, a skala tej jednokładności jest liczbą ujemną SO₁=(16,0) SO₂=(6,4) k=−4 Ale nie wychodzi poprawnie [6−x]=−4[−16−x] [4−y]=−4[0−y]

Mila: r=2 promień mniejszego okręgu R=4 promień większego okręgu

	4
k=−		=−2
	2

Teraz licz.

Radek: Teraz faktycznie wychodzi. Dziękuję.

Mila:

Radek: Dla jakich wartości parametru m równanie x²+y²−2mx+2m−1 = 0 opisuje okrąg? a Podaj wspórzędne środka i długość promienia okręgu. b.Dla jakich wartości parametru m okrąg ten jest styczny do prostej o równaniu x = 4 ? a) (x−m)²+y²=m²−2m+1 (x−m)²+y²=(m−1)² (x−m)²+y²=|m−1| S=(m,0) r=|m−1| b) nie wiem ?

Radek: ?

bezendu: pierwsza część dobrze r=|m−1| inaczej miałbyś promień ujemny

Mila: a) W trzeciej linijce ma być ...=|m−1|² (x−m)²+y²=(m−1)² r=|m−1|, aby to było równanie okręgu musi być m−1≠0⇔m≠1 b)Równanie 4²+y²−2m*4+2m−1 = 0 ma mieć jedno rozwiązanie; dokończysz, czy napisać

Radek: Chcę sam dokończyć tylko skąd to równanie się wzięło ?

Mila: Prosta x=4 i okrąg x²+y²−2mx+2m−1 = 0 mają mieć dokładnie jeden punkt wspólny. W miejsce x do równania okręgu podstawiłam 4.

Radek: Ok.

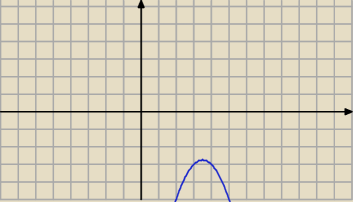
Radek: Wyznacz współrzędne punktu P leżącego na wykresie funkcji y = 7x− x²−15 , dla którego suma odległości od osi układu współrzędnych jest najmniejsza

Mila: P(x,−x²+7x−15) odległości Rzut punktu P na oś OX: M(x,0) Rzut punktu P na oś OY: N(0, −x²+7x−15) Licz sumę odległości] f(x)=|PM|+|PN|

Radek: Dziękuję

Mila: Dobranoc

Radek: Dobranoc.