bez sensu
bezendu:
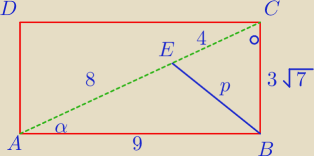
W prostokącie ABCD w którym AB=9 AD=3
√7, na przekątnej AC wybrano taki punkt E, że AE:EC=2:1
Oblicz sinus kąta EBC
kropka u góry 90−α
robię z twierdzenia cosiunsów
p
2=8
2+9
2−2*8*9cosα
p
2=4
2+(3
√7)
2−4*3
√7*sinα
przyrównuje do siebie a p wychodzi kosmiczne
5 kwi 21:27
Damo93: cosα = 9/12 = 3/4
p2 = 64 + 81 − 2 x 8 x 9 x 3/4
p2 = 145 − 108
p2 = 37
p = √37
5 kwi 21:40
bezendu:
Faktycznie. Dziękuję.
5 kwi 21:43
Mila:
No kosmiczne.
Może poprowadź EF równoległą do AB. (Będzie to wysokość w ΔBCE)
| | 4 | | 12 | |
EF=3 z tw. Talesa |
| = |
| |
| | EF | | 9 | |
Oblicz CF, potem FB i ...
5 kwi 21:45
Saizou : Mila właśnie chciałem pisać że z podobieństwa
5 kwi 21:47
bezendu:
Wybiorę jednak sposób Damo
5 kwi 21:48
Mila:
Bardzo dobry sposób.
5 kwi 22:03