geom Radek: Dany jest punkt M = (2 ,8 ) . Wyznacz równanie takiej prostej k , do której należy punkt M , że na ujemnej półosi Ox i dodatniej półosi Oy układu xOy prosta ta wyznacza odcinki OA i OB , których suma długości jest równa 6. Oblicz obwód trójkąta AOB . Proszę o wskazówki

Radek: ?

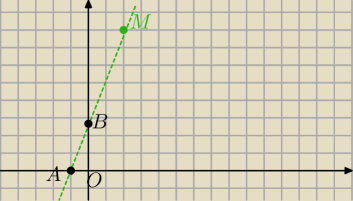
Mila: Podpowiedź. |OA|+|OB|=6 y=ax+b A=(x₀) B(0,b)

J:

2		8
	+		= 1
a		b

a + b = 6 i a< 0

J: a > 0

Radek: Nadal nie wiem ?

J: Wyznacz b z drugiego równania i podstaw do pierwszego, dostaniesz równanie kwadratowe ze zmienną a.

Mila: y=ax+b i M(2,8) należy do prostej⇔ 8=2a+b b=8−2a i b>0⇔8−2a>0⇔a<4 Równanie prostej ma postać : y=ax+8−2a miejsce zerowe ax+8−2a=0 ax=2a−8

	2a−8
x0=		i a>0
	a

	2a−8
|		|+8−2a=6 rozwiązuj,
	a

J: Szukana prosta: y = 2x +4

Radek: Podnieś do do ² ?

Mila: O którym równaniu mówisz?

Radek: o 22:03

Mila: Ponieważ założyliśmy, że 0<a<4 to

	2a−8		8−2a
|		| =		możemy zapisać:
	a		a

	8−2a
		+8−2a=6 /*a
	a

Radek: Te zadania zamiast robić się coraz prostsze to coraz trudniejsze są...

J: I pomału dochodzimy do równania : y = 2x + 4

Radek: Ja nie dochodzę do niczego jak na razie.

J: Jakby nie policzył .. to a = 2 lub a = − 2 ( to odrzucamy) , czyli a =2 i b = 8 − 2a = 4, kropka.Szukana prosta : y = 2x + 4

Mila: Z czym masz problem Radku?

Radek: Ze zrozumieniem tego zadania.

Mila: Którego miejsca w tym co Ci podpowiedziałam?

Radek: Czemu to wszystko jest zależne od a ?

J: Przeczytaj treść zadania. " na ujemnej części osi OX i dodatniej OY" , czyli a > 0