Translacja o wektor - przekształcenia kinigis: Podaj wzór funkcji G(x) w postaci iloczynowej. Funkcję tę otrzymamy, przekształcając wykres funkcji W(x)=−¹₄x⁴+x³−x² przez translację o wektor u=[−1;9]. Właśnie z tą postacią iloczynową mam problem, próbowałam Hornerem, ale nie wychodzi...

J:

	1
G(x) = −		(x+1)4 + (x+1)3 −(x+1)2 + 9
	4

kinigis: do tego momentu mam, ale kiedy wyłączam wspólny czynnik przed nawias i próbuję zrobić w tego postać iloczynową, nic nie wychodzi.

kinigis: a w poleceniu jest właśnie podanie wzoru w postaci iloczynowej

pigor: ..., widzę to np. tak : W(x)= −¹₄x⁴+x³−x²= −¹₄x²(x²−4x+4)= −¹₄x²(x−2)², to w T_[−1,9] masz G(x)= −¹₄(x+1)²(x+1−2)²+9= −¹₄(x+1)²(x−1)²+9= = −¹₄[(x+1)(x−1)]²+9= −¹₄(x²−1)²+9= −¹₄ [(x²−1)²−9] = = −¹₄ (x²−1−3)(x²−1+3)= −¹₄ (x²−4)(x²+2)= −¹₄(x−2)(x+2)(x²+2).

Mila:

	1
f(x)=−		x4+x3−x2
	4

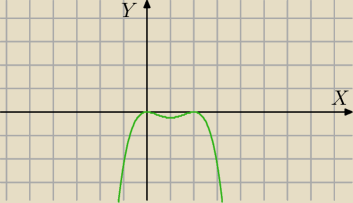
Miejsca zerowe

	1
x2*(−		x2+x−1)=0
	4

x=0 lub x=2

	−1
f(x)=x2*		*(x−2)2
	4

po translacji wykresu o wektor [−1,9] funkcja ma wzór:

	1
g(x)=−		(x+1)4+(x+1)3−(x+1)2 +9 i będzie miała 2 miejsca zerowe.
	4

Podstawienie : t=x+1

	1
g(t)=−		t4+t3−t2 +9
	4

	1
g(t)=9−		*t2*(t−2)2
	4

	1
g(t)=32−[		t*(t−2)]2⇔
	2

	1		1
g(t)=(3−		(t−2)*t)*(3+		(t−2)*t) dokończ, podstaw za t i uporządkuj
	2		2

	1
..g(x)=		*(7−x2)*(5+x2)
	4

pigor: ..., o no to, niech autor tematu mi wybaczy, ale mi się nie chce szukać błędu, chyba, że zrobi to ktoś za mnie; przepraszam..

Mila: W trzeciej linijce na końcu ma być +9, i piękny zapis krótki.

pigor: ..., dzięki, przepraszam mam błąd w wyłączaniu przed nawias ułamka −¹₄ w 2−giej linijce od końca, tu ...=−¹₄(x²−1)²+9= −¹₄[(x²−1)²−4*9] =−¹₄(x²−1−6)(x²−1+6)= = −¹₄ (x²−7)(x+2)(x²+5)= −¹₄ (x−√7)(x+√7)(x²+5) . ...

kinigis: dzieki!

Mila: