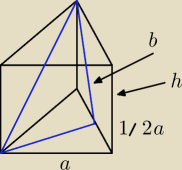
Oblicz objętość graniastosłupa. Janusz: W graniastosłupie prawidłowym trójkątnym poprowadzono płaszczyznę π wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna π z płaszczyzną podstawy graniastosłupa tworzy kąt o mierze α≠90. Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę π jest równe S. Oblicz objętość graniastosłupa. P_przekroju=S

	1
V=		Pp*H
	3

	a2√3
Pp=
	4

	1	a2√3
V=			*H
	3	4

	1	a√3
P=			*b
	2	2

	ab√3
S=
	4

	1
H2+		a2=b2
	4

	1
b2=H2+		a2
	4

16S2		1
	=H2+		a2
3a2		4

	3
16S2=3a2H+		a4
	4

Potrzebuje trzech równań do trzech niewiadomych, nie mam pojęcia jak zrobić to zadanie, pomoże ktoś?

Janusz: up

Janusz: up

Mila: Podpowiedź: 1) Przekrój jest Δ prostokątnym . 2) Dlaczego nie wykorzystujesz tego, że masz dany kąt α? ( Między b i krawędzią podstawy.)

	2H
tgα=
	a

	1
H=		a*tgα
	2

	0,5a
cosα=
	b

Janusz: ok, wszystko sobie zaznaczyłem i teraz to widzę. robię dalej

Mila:

Janusz: dzięki wielkie

Janusz: czyli mam coś takiego: H=2*tgα a=2b*cosα

	1
H2+		a2=b2
	4

teraz muszę się bawić w podstawianie, jak będzie najszybciej? podstawić teraz a,H do równania kwadratowego i wyliczenie b?

Mila: Zrobione?

Janusz: wtedy:

	1
4tg2α+		*4b2*cos2α=b2
	4

b²−b²cos²α=4tg²α b²(1−cos²α)=4tg²α

	4tg2α
b2=
	sin2α

	4
b2=
	cos2α

	2		2
b=		V b=−
	cosα		cosa

Mila:

	1
H=		*a*tgα
	2

b=√H²+(1/4)a²

	1
S=		*hp*b
	2

1		a√3
	*		*√H2+(1/4)a2=S
2		2

Podstaw za H i oblicz a. Dalej działaj.

Janusz:

	a√3		1		1		1
S=		√		a2*tg2α+		a2 wyrażenie od		całe pod pierwiastkiem
	4		4		4		4

	a√3		1		1
S=		√		a2(tg2α+1) wyrażenie od		całe pod pierwiastkiem
	4		4		4

	a√3		a
S=		*		*√tg2α+1
	4		2

	a2√3
S=		√tg2α+1
	8

Mila:

	sinα
Dobrze, podstaw za tgα=
	cosα

	a2√3
wtedy S=		/*cosα
	cosα

i oblicz a.

Janusz: hm? jak to?

	sinα		a2√3
jak podstawiając za tgα=		otrzymamy S=		?
	cosα		cosα

Mogłabyś to rozpisać? Bo ja to widocznie robię źle:

	a2√3		sin2α
S=		=√		+1 − całe wyrażenie pod pierwiastkiem
	8		cos2α

	a2√3		sin2α+cos2α(sin2α+cos2α)
S=		√		wyrażenie pod pierwiastkiem
	8		cos2α

	a2√3		sin2α+sin2αcos2α+cos2α
S=		√		wyrażenie pod pierwiastkiem
	8		cos2α

hm? wracając do obliczenia a,

	√3S*cosα
a2=		, to będę mógł wstawić za Pp
	3

Mila: Pod pierwiastkiem tak:

	sin2α		sin2α+cos2α		1
tg2α+1=		+1=		=
	cos2α		cos2α		cos2α

	8√3*S*cosα
a2=
	3

	a2√3		8√3*S*cosα		√3
Pp=		=		*
	4		3		4

Janusz:

Janusz: o, w tym samym momencie napisaliśmy

Janusz: P_p=2S*cosα

	1		4
V=		*2Scosα*2tgα=		S*cosα
	3		3

Janusz: dzięki wielkie Milu

Mila:

	1
Źle objętość: do H=		a*tgα musisz podstawić za a.
	2

Masz spierwiastkować a².

Janusz: mam na tej kartce już tyle różnych rzeczy, że pomyliłem H,

	S√3*cosα
a=2√2√		całe wyrażenie pod pierwiastkiem
	3

	S√3*cosα
H=√2*tgα*√		całe wyrażenie pod pierwiastkiem
	4

Mila: Właśnie pisanie tutaj tego piętrusa pod pierwiastkiem jest trudne. Jeśli nie masz odpowiedzi, to Ci napiszę.

Janusz:

	2√2		S√3cosα
V=		S*sinα*√
	3		3

Janusz: wcześniej przy H zrobiłem literówkę, jest tam 3 zamiast 4 w mianowniku nie, nie mam odpowiedzi, biorę zadania z internetu i rozwiązuje ile się da

Mila: Dobrze.

Janusz: dzięki ponownie Milu