d DDD: W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość 3 a sinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy jest równy √33/6. Oblicz: a) Długość krawędzi bocznej b) Pole powierzchni całkowitej i objętość c) tangens kąta nachylenia ściany bocznej do płaszczyzny podstawy.

Dounat: Masz może odpowiedzi do tego zadania? Rozwiązałem owe zadanie, ale nie mam pewności czy wszystko dobrze obliczyłem

DDD: Niestety to ze sprawdzianu

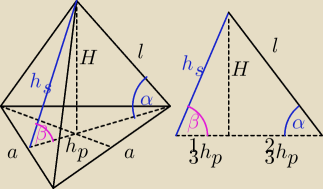
dero2005: a = 3

	H		√33
sinα =		=
	l		6

_________________________

	a√3		3
hp =		=		√3
	2		2

	√3
cosα = √1−sin2α =
	6

2   hp 3		√3
	= cosα =
l		6

l = 6 H = √l² − (²₃h_p)² = √33

	3
hs = √H2 + (13hp)2 =		√15
	2

	a2√3		3		9
Pc =		+		a*hs =		(√3 + 3√15)
	4		2		4

	a2√3*H		9
V =		=		√11
	12		4

	H		2
tgβ =		=		√11
	1   hp 3		3

obliczenia (wyniki) radzę sprawdzić

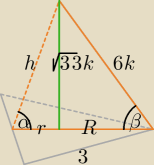Bogdan: Obliczenia są prostsze, jeśli odpowiednio przyjmie się oznaczenia

	1		1		1		3
k > 0, R =		*3*√3 = √3, R2 = 3, r =		R =		√3, r2 =
	3		2		2		4

a) 33k² + 3 = 36k² ⇒ k = 1 ⇒ 6k = 6

	3
b) Wysokość ostrosłupa = √33 * 1 = √33, h = √33 + 3/4 =		√15
	2

	1		1		3		9
P =		*9√3 + 3*		*3*		√15 =		√3(1 + 3√5)
	4		2		2		4

	1		1		9
V =		*		*9√3*√33 =		√11
	3		4		4

	√33
c) tgα =		= 2√11
	√3     2