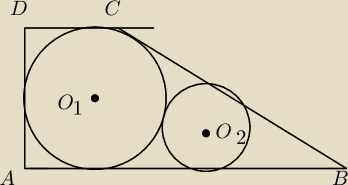
Planimetria, Dwa okręgi wpisane w trapez prostokątny Adr: W trapez prostokątny ABCD wpisano okrąg o środku O₁. Następnie narysowano okrąg o środku O₂, styczny zewnętrznie do pierwszego okręgu oraz styczny do dwóch boków tego trapezu. Wiadomo, że |AB|=28, |BC|=25, |CD|=21, |AD|=24. Oblicz promień mniejszego okręgu. Rysunek może nie jest zbyt dokładny ale chyba wszyscy wiedzą o co chodzi . Ktoś ma jakieś wskazówki do rozwiązania?

kochanus_niepospolitus:

	1
R =		|AD| = 12
	2

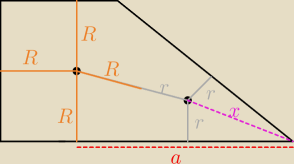
a = 28 − R = 16 a² + R² = (R+r+x)² 16² + 12² = (16+r+x)² −> r+x = 4 z tw. Talesa:

x		R+x+r		20		3
	=		=		−> r =		x
r		R		12		5

	3
r+x = 4 −> r +		r = 4 −> r = .....
	5

Adr: chyba coś jest nie tak bo powinno wyjść 3, a wychodzi ²⁰₈. skąd wiesz, że odcinki R+r+x, to przeciwprostokątna tego trójkąta ? Poza tym w odcinku x zawiera się promień r, więc ten odcinek powinien być chyba dłuższy

Adr: Ma ktoś inny pomysł?

Eta: Zauważ ,że pomyłkowo zamiast R=12 kochanus wpisał 16 tu: 16²+12²= (12+r+x)² ⇒ 12+r+x=20 ⇒ r+x= 8

	3
dalej ok ....... tylko w końcowym obliczeniu: r+		r= 8 ⇒ r=3
	5

Adr: Faktycznie, nie zauważyłem, dzięki

Adr: Ale dalej się coś nie zgadza bo wyjdzie r=5

Adr: Pomoże ktoś?

marta: R=12 , a=16 (R+r+x)²=400 ⇒ 12+r+x=20 ⇒ r+x=8

	R		R+r+x
z tw. Talesa :		=
	r		x

12		20		5
	=		⇒ x=		r
r		x		3

	8
r+x=8 ⇒		r=8 ⇒ r=3
	3