w okrąg o promieniu długości r wpisano kwadrat ABCD kotek: w okrąg o promieniu długości r wpisano kwadrat ABCD . Punkt P jest dowolnym punktem okregu, rożnym od wierzchołków kwadratu . Uzasadnij ze |PA|² +|PB|² + |PC|² + |PD|² = 8r²

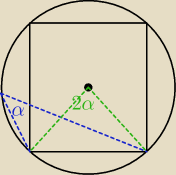
wredulus: 2α = 90 (dlaczego)

	90
stąd: α =		= 45o
	2

z tw. cosinusów: |AB|² = |PA|² + |PB|² − 2*|PA|*|PB|*cos45^o i tak dla każdej 'czwórki' robisz i dostaniesz: |AB|² = |PA|² + |PB|² − 2*|PA|*|PB|*cos45^o |BC|² = |PB|² + |PC|² − 2*|PB|*|PC|*cos45^o |CD|² = |PC|² + |PD|² − 2*|PC|*|PD|*cos45^o |DA|² = |PD|² + |PA|² − 2*|PD|*|PA|*cos135^o = |PD|² + |PA|² + 2*|PD|*|PA|*sin45^o albo kombinuj tak: |PA|² = |PO|² + |OA|² − 2|PO||OA|cosα ... analogicznie pozostałe: suma tych czterech równań: |PA|² +|PB|² + |PC|² + |PD|² = 8r² − 2r²(cosα+cosβ+cosγ+cosδ) przy czym: α+β+γ+δ = 360^o ; β= 90+α oraz γ = 90+δ oraz α+δ = 90^o czyli skorzystaj ze wzorów redukcyjnych i masz: |PA|² +|PB|² + |PC|² + |PD|² = 8r² − 0 c.n.w.