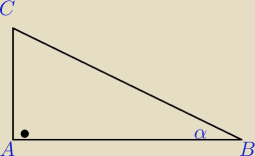
bez sensu chyba bezendu: Jeden z kątów ostrych trójkąta prostokątnego ma miarę α . Oblicz stosunek wysokości poprowadzonej z wierzchołka kąta prostego do promienia okręgu wpisanego w ten trójkąt

AC
	=U{CB}
sinα

	AB
CB=
	sinα

AB
	{cosα}
BC

ABcosα=BC ?

Godzio:

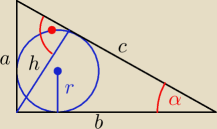
	a + b − c		csinα + ccosα − c
r =		=		= {c}{2} * (sinα + cosα − 1)
	2		2

	ab		ch		ab
P =		=		⇒ h =		= csinαcosα
	2		2		c

h
	= ...
c

bezendu: Ale ja chcę dokonczyć to co ja zacząłem. I pytam się co dalej ?

Godzio: |AC| = a |BC| = c |AB| = b I masz dokończone. Dalej nie kombinujesz sam tylko od razu wrzucasz zadanie na forum.

bezendu: Kombinuje tylko, że każdy boku wychodzi w inaczej a w poleceniu mam tylko kąt α

Godzio: Musisz uzależnić wszystko od jednej liczby i tyle (w tym wypadku uzależniłem od c)

bezendu: I niby czemu a,b,c jak to chyba trzeba uzależnić od kąta α ?

Godzio: Stosunek ma być uzależniony od kąta, a boki a, b i c nie muszą

bezendu: Czyli nie potrzebnie wyznaczałem te boki ?

Godzio: Dobrze wyznaczałeś, ale w zależności od złego boku. Bo to Ci po prostu nic nie da.

bezendu: Dobra, czyli bez oznaczeń.

Mila: W takim zadaniu oznaczaj tradycyjnie boki Δ literami : a, b, c pamietając, że naprzeciw boku a leży kąt α,...

bezendu: No tak, ale miałem podany kąt więc chciałem to uzależnić od tego kąta.

Mila: I dobrze, ale jeszcze trzeba wybrac do tego jakiś bok. (jeden, bo w iloazie ma się uprościć) Wiesz ,że wysokość obliczysz z porównania pól a do tego potrzebne boki. Wysokość ma być opusczona na przeciwprostokątna, to wybierasz właśnie ten bok.

bezendu: \Wszystko od boku BC ?

Mila:

	a
sinα=
	c

cosα=...

bezendu: b/c

Mila: Co to jest b/c ?

bezendu: Cosalfa

Mila: Nie załamuj mnie, to masz wiedzieć w nocy o pólnocy, po 3 piwach. Dalej rozwiązuj.

bezendu: Przyprostokątna przy kącie do przeciwieprostokątnej. Więc czym niby załamuje?

Mila: To jest dobrze, ale ja oczekuję na dalszy ciąg.

bezendu: teraz wzór na r ?

Mila: h obliczyłeś? To podaj.

bezendu: h=sin²αc

bezendu: h/r= cosα+sinα+1 ?

Mila: h=c*sinα*cosα

h
	dobrze.
r

Domel: Sprawdzam obliczenia. Ale na przyszłość w podobnych zadaniach uzależnij wszystko od zadanego kąta i max jednej ściany np. przyjmujemy „a”: b = a*ctgα

	a
c =
	sinα

P_Δ = ... i tak dalej. Zapewne powiadam wam (ale to brzmi pięknie − jak na kazaniu Ojca Dyr. ) a się pewnie uprości i zostaną same funkcje od α

Mila: Domelku, to samo napisałam nieco wyżej.

bezendu: W h błąd bo cosalfasinalfac

Domel: A ja pisałem bez odświeżania − no i dlatego zadziałałem jak echoooooooo

Mila: II sposób : Prawie Nic nie trzeba liczyć, tylko znać wzory.

	a+b+c
PΔ=		*r
	2

	1
PΔ=		*c*h
	2

a+b+c		1
	*r=		*c*h⇔
2		2

(a+b+c)*r=c*h /:c /:r

a+b+c		h
	=		⇔
c		r

a		b		h
	+		+1=
c		c		r

	h
sinα+cosα+1=
	r

Mila: III sposób

bezendu: Dziękuję.

as: akii rysunek tojedst to \ '

Rajuu: Chciałabym się Was o coś zapytać odnośnie tego zdania

	c
r=		*(sinα+cosα−1)
	2

h=csinαcosα

h		2		2sinαcosα
	=csinαcosα *		=		...
r		c(sinα+cosα−1)		sinα+cosα−1

	h
nie rozumiem skąd się wzięło, że ostatecznie		=sinα+cosα+1
	r

Mila: To są równoważne wyniki:

2*sinx*cosx		(sinx+cosx)+1
	*
(sinx+cosx)−1		(sinx+cosx)+1

	2sinx cosx*(sinx+cosx+1)
=		=
	sin2x+2sinx*cosx+cos2x−1

	2sinx cosx*(sinx+cosx+1)
=		=sinx+cosx+1
	1+2sinx cosx −1

Rajuu: Dziękuję za odpowiedź! Miłej nocy!

Mila: Wzajemnie.