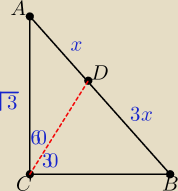
W trójkącie ABC Damo93: W trójkącie ABC mamy dane AC= √3 i kąt C − 90⁰. Przez wierzchołek C poprowadzono prostą, która utworzyła z bokiem AC kąt 60⁰ i przecięła bok AB w punkcie D tak, że AD : DB = 1 : 3 Oblicz AB , BC i CD Zapisałem to tak jak na rysunku, CB = √16x² −3 i próbowałem to policzyć z tw. cosinusów ale strasznie brzydko to wychodzi..

zawodus: Jakiś sposób to 2 razy cosinusy i pitagoras ale liczyć mnie się nie chce

Saizou : a czy takie 'cuś' w ogóle istnieje

th: Kąt ADC = α.

√3		x
	=
sinα		sin60

CB		3x
	=
sinα		sin30

zawodus: Jak na razie 2 równania i 3 niewiadome. Saizou geogebra sprawdzi

Damo93: Saizou istnieje Kupiłem próbne arkusze maturalne pana Pazdro. i to zadanko to chyba jedno z prostszych jest bo za 4pk. ogólne to poziom w porównaniu z maturą jest hardkorowy !

Marcin: A czasem nie odwrotnie? Na przeciwko 60st nie moze być mniejsza długość niż na przeciwko 30 st.

Saizou : Marcin też tak myślałem dlatego napisałem że nie istnieje, ale jeśli narysuje się odpowiednio duży trójkąt to się da xd

Marcin: O prosze Ten rysunek Damo93 mnie zwiódł

Saizou : mnie niestety też

Damo93: ,,Planimetria to sztuka liczenia właściwych wartości z zle narysowanych rysunków.." czy jakoś tak to leciało

Saizou : rysunek to podstawa jak dla mnie

Marcin: Pierwsze słyszę ale za to wiem, że rysunek to połowa sukcesu

marta: "porządny rysunek,to połowa sukcesu"

zawodus: To liczymy