stereometria
Estrella: Oblicz miarę kąta między sąsiednimi ścianami bocznymi ostrosłupa.
Wysokość ostrosłupa prawidłowego czworokątnego jest równa 10, a krawędź podstawy ma długość 8.
Oblicz (z dokładnością do 1 stopnia ) miarę kąta zawartego między wysokościami sąsiednich ścia
bocznych tego ostrosłupa opuszczonymi na przeciwległe krawędzie boczne.
4 kwi 13:05
Estrella: pomoze, ktos

4 kwi 13:19
Estrella: pliss
4 kwi 13:34
mm: Oblicz długość krawędzi bocznej i wysokość ściany bocznej opuszczonej na krawędź boczną.
4 kwi 13:42
Estrella: dł krawedzi bocznej mi wyszla: 2√33
a wysokosc: 2√29
4 kwi 13:46
Estrella: i to sa jakies bzdury...

4 kwi 14:02
mm: Masz odpowiedzi

4 kwi 14:02
mm: Mi kąt między dwoma sąsiednimi ścianami bocznymi wyszedl 98 stopni.
4 kwi 14:07
mm: Ale mi się wydaje że to inny kąt w tym zadaniu trzeba obliczyc
4 kwi 14:08
Estrella: powinno wyjsc 44 stopnie
4 kwi 14:22
Estrella: nwm jak to obliczyc

4 kwi 14:23
Estrella: 
4 kwi 14:26
Estrella: wie ktos jak to policzyc

ktos madry z mat

4 kwi 14:27
zawodus: ktoś wie

4 kwi 14:29
J: Czy Ty dobrze przepisałaś treść zadania ?
... "miarę kąta zawartego między wysokościami sąsiednich ścian bocznych tego ostrosłupa
opuszczonymi na przeciwległe krawędzie boczne" − troche do dziwne ?
4 kwi 14:30
ICSP:
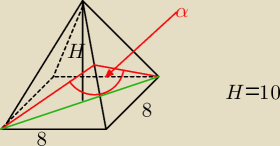
i teraz możemy zacząć rozmawiać.
Słucham twoich propozycji
4 kwi 14:33
Estrella: powinno tak byc:
miarę kąta zawartego między wysokościami sąsiednich ścian tego ostrosłupa
opuszczonymi na przeciwległe krawędzie boczne
4 kwi 14:34
Estrella: coz wyobrazalam sb ten rysunek nieco inczej, a co za tym idzie inaczej narysowalam...
4 kwi 14:34
Estrella: twoj rysunek ulatwia sprawe

4 kwi 14:35
ICSP: źle narysowałem : /
Jeszcze raz.
4 kwi 14:36
Estrella: ae niezupelnie...
4 kwi 14:37
ICSP:

4 kwi 14:38
J: ... na przeciwległą krawędź boczną .. ( a nie krawędzie )
4 kwi 14:38
J: teraz gra..
4 kwi 14:39
Estrella:
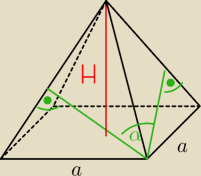
ja to tak narysowalam:
4 kwi 14:40
Estrella: mozna policzyc krawedz boczna, przekatna podstawy, wysokosc ciany bocznej, ale to sa kosmiczne
liczby

4 kwi 14:42
Estrella: krawedz boczna 2√33
wysokosc sciany bocznej 2√29
4 kwi 14:43
Estrella: przekatna podstawy 8√2
4 kwi 14:43
Estrella: co z tym dalej zrobic to ja nie mam pojecia
4 kwi 14:44
mm: Wysokość ściany bocznej opuszczona na krawędź boczną.
4 kwi 14:44
Estrella: 
4 kwi 14:46
Estrella: ja sie poddaje, nie mam tyle czasu, zeby siedziec nad jednym zadaniem pol dnia...

4 kwi 14:47
Estrella: prosze, rozwiazcie mi to zadaie, bo ja nie dam rady sama

4 kwi 14:54
Estrella: prosze
4 kwi 15:06
mm: Nie wychodzi mi 44 stopnie
4 kwi 15:07
Estrella: dzieki, wielkie za pomoc (za narysowanie rysunku, ktory juz dawno narysowalam)
4 kwi 15:07
Estrella: mi tez nie
4 kwi 15:07
Estrella: i to powod mojej prosby o pomoc
4 kwi 15:07
Estrella: powinno wyjsc około 44
4 kwi 15:08
mm: Ile ci wychodzi
4 kwi 15:08
Estrella: ja nawet nie doszlam do kata
4 kwi 15:32
mm: oblicz druga wysokosc sciany bocznej
4 kwi 15:34
Domel:
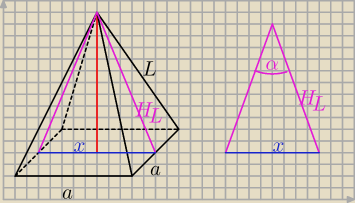
H = 10; a = 8; L = 2
√33; H
L = 2
√29
x = a
Z twierdzenia cosinusów:
a
2 = 2H
L2 − 2H
L2*cosα = 2H
L2*(1 − cosα)
64 = 2*116*(1 − cosα)
| | 64 | | 8 | | 21 | |
cosα = 1 − |
| = 1 − |
| = |
| = 0,724138 |
| | 232 | | 29 | | 29 | |
α = 43,6° = ~44°
4 kwi 17:36
th: Mógłbyś wytłumaczyć dlaczego taki rysunek
4 kwi 17:50
Domel:
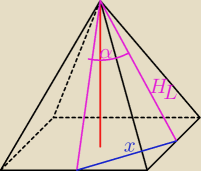 Estrella:
Estrella: napisała
Wysokość ostrosłupa prawidłowego czworokątnego jest równa 10, a krawędź podstawy ma długość 8.
Oblicz (z dokładnością do 1 stopnia ) miarę kąta zawartego między wysokościami sąsiednich ścia
bocznych tego ostrosłupa opuszczonymi na przeciwległe krawędzie boczne.
Opis zagmatwany więc liczyłem dla różnych przypadków szukając gdzie wychodzi 44° podane w
odpowiedzi. Gdy liczyłem wg rysunku
Estrelli z 14:40, to kąt wychodził ok 70°.
Gdy liczyłem wg rysunku który teraz dołączam − to kąt wychodził ok 39°.
I tylko wg rysunku z 17:36 wychodzi 44°
4 kwi 18:10
th: dzięki
4 kwi 18:22
Estrella: dzięki

6 kwi 22:37





 ktos madry z mat
ktos madry z mat 

 i teraz możemy zacząć rozmawiać.
Słucham twoich propozycji
i teraz możemy zacząć rozmawiać.
Słucham twoich propozycji


 ja to tak narysowalam:
ja to tak narysowalam:




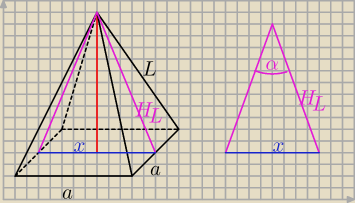 H = 10; a = 8; L = 2√33; HL = 2√29
x = a
Z twierdzenia cosinusów:
a2 = 2HL2 − 2HL2*cosα = 2HL2*(1 − cosα)
64 = 2*116*(1 − cosα)
H = 10; a = 8; L = 2√33; HL = 2√29
x = a
Z twierdzenia cosinusów:
a2 = 2HL2 − 2HL2*cosα = 2HL2*(1 − cosα)
64 = 2*116*(1 − cosα)
 Estrella: napisała
Wysokość ostrosłupa prawidłowego czworokątnego jest równa 10, a krawędź podstawy ma długość 8.
Oblicz (z dokładnością do 1 stopnia ) miarę kąta zawartego między wysokościami sąsiednich ścia
bocznych tego ostrosłupa opuszczonymi na przeciwległe krawędzie boczne.
Opis zagmatwany więc liczyłem dla różnych przypadków szukając gdzie wychodzi 44° podane w
odpowiedzi. Gdy liczyłem wg rysunku Estrelli z 14:40, to kąt wychodził ok 70°.
Gdy liczyłem wg rysunku który teraz dołączam − to kąt wychodził ok 39°.
I tylko wg rysunku z 17:36 wychodzi 44°
Estrella: napisała
Wysokość ostrosłupa prawidłowego czworokątnego jest równa 10, a krawędź podstawy ma długość 8.
Oblicz (z dokładnością do 1 stopnia ) miarę kąta zawartego między wysokościami sąsiednich ścia
bocznych tego ostrosłupa opuszczonymi na przeciwległe krawędzie boczne.
Opis zagmatwany więc liczyłem dla różnych przypadków szukając gdzie wychodzi 44° podane w
odpowiedzi. Gdy liczyłem wg rysunku Estrelli z 14:40, to kąt wychodził ok 70°.
Gdy liczyłem wg rysunku który teraz dołączam − to kąt wychodził ok 39°.
I tylko wg rysunku z 17:36 wychodzi 44°
