2 kwi 23:15
Marcin:
1.
a
1=1
a
1+
1=1−a
1=1−1=0
a
2+1=1−a
2=1−0=0
Ciąg wygląda tak:
1,0,1,0,1,0 ..

2 kwi 23:22
Bogdan:
A zapisać można tak:
Zbadaj monotoniczność ciągu (an): a1 = 1 i an+1 = 1 − an
Ciąg nie jest monotoniczny
2 kwi 23:27
Marcin: Tak widzę, że napisałem 1−0=0

to nieprawda, żeby nie było nieporozumień

2 kwi 23:30
Bogdan:
Drugie zadanie:
| | an+1 | |
Zbadaj monotoniczność ciągu (an): a1 = 1 i an+1 = 2an ⇒ |
| = 2 |
| | an | |
Jaki to ciąg, rosnący, malejący, czy inny?
2 kwi 23:30
kalaaa: rosnący
2 kwi 23:33
kalaaa: ale skąd w tym 1 wiadomo od razu ze nie jest monotoniczny?
2 kwi 23:34
Bogdan:
bo a1 = 1, a2 = 0, a3 = 1 i to wystarczy do stwierdzenia, że ciąg nie jest monotoniczny
2 kwi 23:35
Marcin: Ciąg może być albo rosnący, albo malejący, albo stały. Wtedy jest monotoniczny.
2 kwi 23:35
Bogdan:
Jeśli ciąg jest stały, to nie jest monotoniczny. Ciągi monotoniczne to ciągi:
rosnące, malejące, nierosnące, niemalejące.
2 kwi 23:37
kalaaa: wiem wiem

tylko czy ja moge sobie tak postawiać a nie na wyrazach ogólnych?
2 kwi 23:37
2 kwi 23:38
Marcin: No w sumie masz rację Bogdanie

2 kwi 23:38
kalaaa: bo z tego co jest tam nic a nic nie czaje

2 kwi 23:39
kalaaa: Dla jakich wartości parametru b ciąg an ma granicę równą 2?
an= bn/(b+1)n+3
an= b2n/ (b+4)n+b
2 kwi 23:40
kalaaa: pomózcie prosze bo zaraz się tu rozpłaczę:(
2 kwi 23:41
Bogdan:
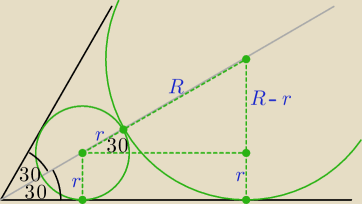
| R − r | | R − r | | 1 | |
| = sin30o ⇒ |
| = |
| ⇒ 2R − 2r = R + r ⇒ R = 3r |
| R + r | | R + r | | 2 | |
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
Niech r
1 to długość promienia najmniejszego okręgu, r
2 − długość promienia drugiego
okręgu, itd.
r
2 = 3r
1, r
3 = 3r
2 = 9r
1. r
4 = 3r
3 = 27r
1 i r
4 = 2
| | 2 | | 2 | | 6 | | 2 | | 18 | |
27r1 = 2 ⇒ r1 = |
| , r2 = 3* |
| = |
| , r3 = 9* |
| = |
| , |
| | 27 | | 27 | | 27 | | 27 | | 27 | |
| | 2 | | 6 | | 18 | | 54 | |
2πr1 + 2πr2 + 2πr3 + 2πr4 = 2π( |
| + |
| + |
| + |
| ) = ... |
| | 27 | | 27 | | 27 | | 27 | |
3 kwi 01:02
Bogdan:
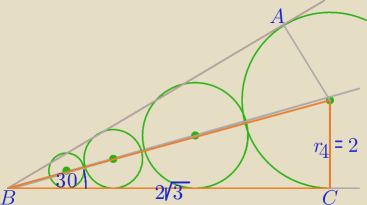
|AB| = |BC| = 2
√3 ⇒ r
4 = 2 (dlaczego?)
3 kwi 01:02

 to nieprawda, żeby nie było nieporozumień
to nieprawda, żeby nie było nieporozumień 
 tylko czy ja moge sobie tak postawiać a nie na wyrazach ogólnych?
tylko czy ja moge sobie tak postawiać a nie na wyrazach ogólnych?



 |AB| = |BC| = 2√3 ⇒ r4 = 2 (dlaczego?)
|AB| = |BC| = 2√3 ⇒ r4 = 2 (dlaczego?)