trójkąt
Loki: W trójkącie ABC w którym |AC|=|BC| = 15 cm i kąt przy wierzchołku C ma miarę 30 stopni
poprowadzono odcinek AD w ten sposób, że D należy do boku BC oraz pole trójkąta ADC jest dwa
razy większe od pola trójkąta ABD. Oblicz |AD|.
2 kwi 21:56
Loki: ma ktoś pomysł ?
2 kwi 22:03
Loki: ?
2 kwi 22:13
Eta:
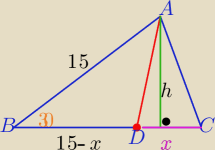
|DC|=x , |BD|=15−x , x∊(0,15)
trójkąty ABD i ADC mają wspólną wysokość h opuszczoną na podstawę BD
z treści zadania :
| | 1 | | 1 | |
|
| *(15−x)*h= 2 * |
| *x*h ⇒ ....... x=5 |
| | 2 | | 2 | |
z tw. kosinusów w trójkącie ABD
|AD|
2=.........
2 kwi 22:50
pigor: ..., widzę to np. tak : z warunków zadania
|AD|=? :
i
PΔADC= 2PΔABD ⇔
12|CD|*h= 2*
12(15−|CD|)*h ⇔
⇔ |CD|=2(15−|CD|) ⇔ |CD|=30−2|CD| ⇔ 3|CD|=30 ⇔
|CD|=10,
stąd, z ΔADC i tw. cosinusów: |AD|
2=15
2+10
2−2*15*10*cos30
o ⇔
⇔
|AD|2=15
2+10
2−2*15*10*cos30
o= 9*5
2+4*5
2−2*15*10*
12√3=
= 13*5
2−6*5
2p{3]=
52(13−6√3) ⇒
|AD|=5√13−6√3 ≈ 3 cm.
2 kwi 22:54
pigor: ...oczywiście mialo być nie 3 tylko 13 ; przepraszam
2 kwi 22:57
Eta:
2 kwi 23:26
Mila:
Cześć Eto, jak zdrówko?
Coś nam 5−latek zniknął z forum.
2 kwi 23:29
Loki: dzięki za odpowiedź
3 kwi 22:30