pomocy
Radek:
Wysokość stożka podzielono na trzy równe odcinki i przez punkty podziału poprowadzono
płaszczyzny równoległe do podstawy. Oblicz stosunek objętości powstałych brył.
2 kwi 20:21
zawodus: Zrób rysunek trójkąta i proste równoległe a potem podobieństwo
2 kwi 20:24
wmboczek: skala objętości to k3
najmniejszy stożek ma 1/27, środkowy 8/27 i dalej wynika z tego ...
2 kwi 20:24
Radek:
ale jak będzie z promieniem ?
2 kwi 20:28
zawodus: To napisz teraz objętość każdego stożka
2 kwi 20:31
Radek:
Ale jak będą promienie ?
2 kwi 20:35
zawodus: Proporcjonalne − z podobieństwa.
2 kwi 20:37
Mila:
Licz z podobieństwa. Wtedy nie pomylisz się.
2 kwi 20:40
Radek:
Ale jak to zaznaczyć na rysunku ?
2 kwi 20:41
zawodus: Normalnie zaznacz ten na dole promień r i wysokość całego H.
2 kwi 20:46
Radek:
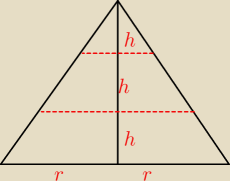
2 kwi 20:48
Mila:
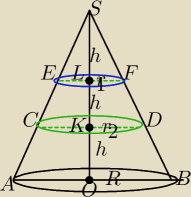
|SL|=|KL|=|KO|=H=3h
V− objętość stożka ABS
| | h | | 1 | | 1 | |
ΔEFS∼ΔABS w skali k= |
| = |
| ⇔r1= |
| R |
| | 3h | | 3 | | 3 | |
I możesz liczyć objętości
Lepiej skorzystać z własnośći:
Stosunek objętości brył podobnych jest równy sześcianowi skali podobieństwa
(to znaczy zwiększysz bryłę 2 razy to objętość zwiększy się 8 razy,
zwiększysz bryłę 3 razy to objętość zwiększy się 27 razy)
stąd:
| Vst.EFS | | 1 | | 1 | |
| =( |
| )3= |
| |
| Vst.ABS | | 3 | | 27 | |
Wybierz sposób i licz.
2 kwi 20:57
zawodus:
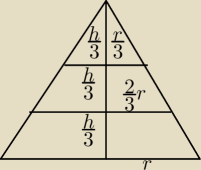
2 kwi 20:59
zawodus: a ja się męczyłem z rysunkiem i w porównaniu do rysunki
Mili mój jest do...
2 kwi 20:59
Radek:
Pierwszy sposób.
2 kwi 21:02
Radek:
Dziękuję, a mam jeszcze pytanie zostało mi jeszcze ponad 500 zadań więc co robić bryły czy
geometrię analityczną tak aby się wyrobić i zrozumieć ?
2 kwi 21:16
Mila:
Mieszaj problemy.
2 kwi 21:17
Radek: Znajdź równanie prostej k przechodzącej przez punkt P(2 ,5) , która ogranicza wraz z dodatnimi
półosiami układu współrzędnych trójkąt o polu równym 36.
2 kwi 21:40
zawodus: Pytanie 1
Jaki trójkąt powstanie?
Pytanie 2
Jak liczymy pole takiego trójkąta?
2 kwi 21:41
Radek:
Trójkąt prostokątny. Ze wzoru na wyznaczniki ?
2 kwi 21:43
zawodus: Można. To teraz potrzebujesz dwóch wektorów.
Zrób rysunek przykładowy i zaznacz te wektory
2 kwi 21:46
Mila:
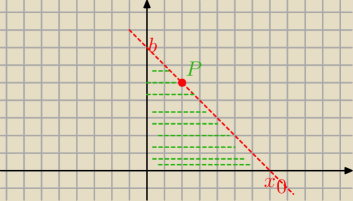
k: y=ax+b
5=2a+b
b=5−2a , b>0
Podobne rozwiązywaliśmy.
2 kwi 21:46
Radek:
Napisz równanie okręgu opisanego na trójkącie o wierzchołkach A = (− 8,− 5) , B = (8,3) i C =
(6,9)
Układ równań ?
2 kwi 21:49
bezendu:
Tak, układ równań trzeba stworzyć, albo jeszcze druga opcja
Pomyśl jaka ?
2 kwi 22:07
Mila:
1) Podstawiasz wsp. punktów do równania :
(x−a)2+(y−b)2=r2
i masz układ równan.
Albo
2) piszesz symetralne dwóch boków Δ, potem znajdujesz punkt przecięcia prostych(środek)
Potem promien.
2 kwi 22:10
zawodus: Dwie symetralne i przeciąć = spodek
Promień to już formalność.
Ciekawe czy czytam w myślach bezendu
2 kwi 22:11
bezendu: Tak, ale zostawiłem to do namysłu nie Tobie
Zawodus 
2 kwi 22:12
zawodus: Nie ja napisałem pierwszy a mnie się oberwało
2 kwi 22:13
Radek:
A jak na tych samych danych napisać równanie okręgu wpisanego w ten trójkąt ?
2 kwi 22:15
zawodus: A jak się konstruuje okrąg wpisany w trójkąt?
2 kwi 22:19
Mila:
To ja Was zostawiam.
2 kwi 22:21
Radek: Dwusieczne
2 kwi 22:22
zawodus: No to dwie dwusieczne i przecinasz i masz środek
2 kwi 22:26
Radek:
Wierzchołek kąta znajduje się w punkcie W = (0,0) , jedno z jego ramion leży na prostej y = 43x
, a drugie ramię przechodzi przez punkt A = (4;− 3) . Punkt P = (7,1) należy do wnętrza tego
kąta. Sprawdź rachunkowo, czy punkt P leży na dwusiecznej tego kąta.
2 kwi 22:34
zawodus: Dwusieczna = zbiór punktów równoodległych od ramion kąta
2 kwi 22:37
Radek:
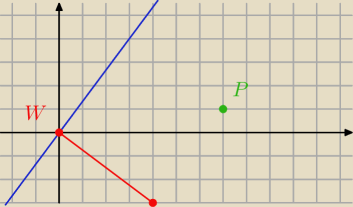
2 kwi 22:38
zawodus: Co to za prosta?
2 kwi 22:42
zawodus: Liczysz odległość P od obu prostych jeśli są te same to leży on na dwusiecznej.
2 kwi 22:44
Radek:
źle napisałem w poleceniu i poprawiłem
dobrze już liczę
2 kwi 22:46
zawodus: Ja już idę spać. Myślę że nie będzie problemów.
2 kwi 23:13
Radek: Dziękuję za pomoc
2 kwi 23:15