aa Hugo: wyznacz wszystkie rozw w przedziale <0; 2π> 2sin² x cosx=sinx 2sin² xcosx= sinx / :sinx sin2x = 1 2x =1

	π
x =
	6

czy to mam dobrze trzeba jakies stwierdzenia

J: Nie możesz podzielić przez sinx , bo przyjmuje w tym przedziale wartośc 0

Hugo: wiec co proponujesz ; /

J: ⇔ 2sin²xcosx − sinx = 0 ⇔ sinx(2sinxcosx − 1) = 0 ⇔ sinx(sin2x −1) = 0

Hugo: :(

Hugo: ogarniam

J: W czym problem ?

Marcin: sinx=0 sin2x−1=0

Hugo: dz to bedzie: x = { 0; π/6 ; 5/6π; π : 2π }

Hugo: czasem rowarzyszu J piszemy w tym samym czasie i post z pytajnikiem nie zamierzony

Hugo: mam jeszcze taki pod pkt D: 4tgxcos² x=1 4sinxcosx=1 sin2x=1/2 x=1/4

	π
czy to sie da jakos przedstawic w formie		... ?
	?

jestem w liceum ale jak na studiach sa jakies sposoby to chetnie sie wdroze

Hugo: :(?

Mila: Masz błąd. 4sinx*cosx=1 2*(2sinx*cosx)=1

	1
sin(2x)=
	2

	π		5π
2x=		+2kπ lub 2x=		+2kπ
	6		6

	π		5π
x=		+kπ lub x=		+kπ
	12		12

Hugo: Milo ty rowniez.zaliczylas mikro bladzik ; przedzial <0;2pi> xd .. dziekuje za objasnienie; niby takie banalne a czlowiek nie wpadnie ... Milo! co do ost naszego spotkania to rozwiazalem tamto, wiem ze czekalas ja liczylem i wstawilem pozniej i chyba dobrze; nie chce bys myslala ze cie olalem; moją najwspanialsza promotorkę Milę !

Mila: A po co tak napisałam? Właśnie masz dokończyc, to zadanie. ( chodziło mi o sprostowanie

	1
		)
	4

Rozwiązania nie są jeszcze wyznaczone. Czekam.

Hugo: heh.. wybacz. wiec : )) x = { π/12 ; 5/12π ; 13/12π ; 17/12π }

Mila: No i pięknie. Czasem jest równanie : na początku x∊<0,2π> W takim

	1
sinx=		nie trzeba dodawać +2kπ, wiadomo są dwa rozw. które podajemy i koniec.
	2

a w takim

	1
sin(4x)=		, piszemy
	2

	π		5π
4x=		+2kπ lub 4x=		+2kπ i będzie sporo rozwiazań.
	6		6

Hugo: mam takie kolejne i kazdy mi przyklad wyszedl poza f) Rozwiaz rownanie: √3cos2x + 9cosx+ 4√3=0 √3cos² x − √3sin² x +9cosx+ 4√3 z jedynki tryg (3+√3)cos² x+9cosx+3√3=0 cosx:=t (3+√3)t²+9t+3√3=0 i mam pytanie; czy do tego momentu mam dobrze? bo delta jest bardzo dziwna

Hugo: twe pochlebstwa napierają mnie dumą! z faktu ze jednak chyba cos umiem i napisze jakos te mature.

ZKS: cos(2x) = 2cos²(x) − 1

Hugo: jak to zlozyles do takiej formy o.o?

Marcin: Tablice matematyczne, strona 15

Hugo: nie posiadam chodz kazali mi kupic A ktos byl by tak dobry i podlinkowal ?

Marcin: Ależ pewnie łap: http://www.cke.edu.pl/images/stories/Tablice/tablice_matematyczne.pdf

Mila: w linijce po słowach z jedynki ma być: 2√3 cos²x+9cosx+3√3=0 Ja zrobiłabym tak: √3cos(2x) + 9cosx+ 4√3=0 /*√3 3cos(2x)+9√3cosx+12=0 /:3 cos(2x)+3√3 cosx+4=0 2cos²x+3√3cosx+3=0, cosx=t,t∊<−1,1> 2t²+3√3t+3=0 Δ=27−24=3

	−3√3−√3
t=		=−√3∉D
	4

	−3√3+√3		√3
lub t=		=−		⇔
	4		2

	√3
cosx=−
	2

dokończ

Marcin: Lub jak proponował ZKS 2√3cos²x+9cosx+3√3=0 cosx=t t∊<−1;1> 2√3t²+9t+3√3 √Δ=3 x₁=−√3 odpada.

	√3
x2=−
	2

Hugo:

	√3
cosx=−
	2

x = 7/6π +2kπ v x = 5/6π+2kπ mam nadzieje ze dobrze ;x narsowalem sobie cosinusoide

Marcin: Wysłałem Ci tablice, tam masz cosinusoide

Mila: Hugo , ostatni typ równania elementarnego dla cosinusa rozwiązujesz tak:

	√3		π		−π
cosx=		⇔x=		lub x=		i teraz stosujesz przesunięcie o π.
	2		6		6

	√3		π		−π
cosx=−		⇔x=		+π+2kπ lub x=		+π+2kπ
	2		6		6

	7π		5π
x=		+2kπ lub x=		+2kπ
	6		6

Hugo:

	√3
ogarnalem! ale tu mamy: cosx= −		czyli cos30 czyli π/6 i na wykresie widac
	2

	√3
symetrycznie co π/6 wokol π argumenty pasujace do wartosci −		+2kπ okresu bo one sie
	2

nie pokrywaja przEz okres, stad 2 rozw

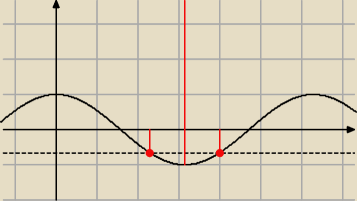
Marcin: Ja sobie zawsze rysuuje

Hugo: Ok Milo i Marcinie no zawsze trzeba sb narysowac i tam widac, jednak wynik mialem dobry co cieaszy. Poprosil bym Mile o jedno zadanko bo nawet mam ochote gdyz Prawdziwy mistrz jest wiecznym uczniem ale rowniez wiemy ze cytujac: "Slodki sen dla pracujacego" ... uciekam spac; mam nadzieje ze i jutro sie spotakmy Dziekuje Wam

Mila: Wszystkie rozwiązania równania : 2cos²x=cosx , x∊<0,2π>

Marcin: 2cos²x−cosx=0 cosx(2cosx−1)=0 2cosx=1

	1
cosx=		cosx=0
	2

Hugo poszedł spać Milo

Mila: Dobranoc.