rownanie liniowe z parametrem k wojtek: cześć, zadanie konkursowe z etapu rejonowego, rocznik 2004 wyznacz liczbe pierwiastkow rzeczywistych rownania x*|x|=x+k w zależności od parametru k. i teraz jak? x*|x| − x =k x*(|x|−1|)=k i po kolei rozważyć 3 przypadki (jedno rozwiazanie, nieskonczenie wiele i brak) ? prosze o wskazowke, bo zrobilem tak ale wtedy wychodza te 3 rozwiazania ale rowniez w zależności od x

muflon: Spróbuj graficznie

muflon: xIxI−x=k rozważ 2 przypadki

muflon: btw jaki to konkurs gimnazjalny?

wojtek: nie, to jest klasy drugie liceum i trzecie technikum

wojtek: dziekuje zaraz sprobuje

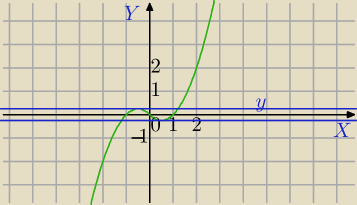
Mila: Metoda graficzna. f(x)=x*|x|−x 1) |x|=x dla x≥0 wtedy funkcja ma postać: f(x)=x²−x

	1		1
x w=		, yw=−		−współrzędne wierzchołka paraboli
	2		4

x=0 lub x=1 miejsca zerowe szkicujemy, parabola skierowana do góry. 2) |x|=−x dla x<0 wtedy funkcja ma postać: f(x)=−x²−x

	1
xw=−
	2

	1
yw=
	4

Szkicujemy. ( ważne wsp. wierzchołków) 2) f(x)=k równanie ma :

	1
Dla k<−		jedno rozwiązanie ( jeden punkt przecięcia wykresu przez prosta y=k i
	4

	1
k<−
	4

	−1
Dla k=		2 rozwiązania
	4

	−1		1
dla k∊(		,		) 3 rozwiązania
	4		4

	1
Dla k=		2 rozwiązania
	4

	1
Dla k>		jedno rozwiązanie
	4

Mila: Wojtek to nie jest równanie liniowe.

wojtek: ok dziekuje bardzo zrobiłem i mam podobne wyniki, już wiem co nie tak

Mila: