graniastosłup
zawodus: bezendu graniastosłup
Dany jest graniastosłup prawidłowy trójkątny o krawędzi podstawy równej 2√3 i wysokości równej
3. Graniastosłup ten przecięto płaszczyzną zawierającą krawędź podstawy i nachyloną do
płaszczyzny podstawy pod kątem 60 stopni. Obliczu pole otrzymanego przekroju.
2 kwi 08:26
bezendu:
Zawodus robiłem już to zadania w innym temacie. Wrócę ze szkoły to zrobię jeszcze raz
2 kwi 09:32
zawodus: Ale ty to napisałeś jak by to był trójkąt, a tak nie jest.
2 kwi 09:36
Piotr 10: bedzie to trapez rownoramienny
dluzsza podstawa 2√3
wysokosc trapezu 2√3
krotsza podstawa 2√3 − 2 ?
2 kwi 12:54
zawodus: Przykro mi, ale poczekamy na
bezendu 
nie chcę mu odbierać przyjemności samodzielnego
rozwiązania
Jak chcesz to mogę wrzucić zadanko dla ciebie
2 kwi 13:27
Piotr 10: Ja chcialem sie zapytac tylko czy mam dobrze, nie dziś. Polski czeka
2 kwi 13:53
Piotr 10: Ale jak chcesz to wrzuć zadanko, tylko takie z poziomu maturalnego, poprosze, to w wolnej
chwili postaram sie zrobic
2 kwi 13:54
zawodus: masz osobny temat
Piotrek
2 kwi 14:20
bezendu:
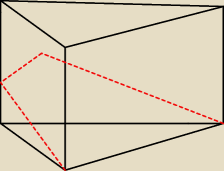
Takie coś ?
2 kwi 15:24
zawodus: Bezendu rysunek do... Rysuj jeszcze raz
ten jeden wierzchołek na czym się trzyma?
2 kwi 20:36
bezendu:
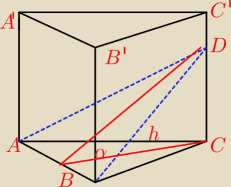
2 kwi 20:38
zawodus: Podałem ci rano, że ro nie jest trójkąt. Może tak .
Jaką figurą może być przekrój przechodzący przez krawędź podstawy?
2 kwi 20:49
bezendu:
To nie wiem jak inaczej to mam narysować.
Trójkąt albo trapez
2 kwi 20:51
zawodus: No dobrze, a od czego to zależy czy trójkąt czy trapez?
2 kwi 20:55
Saizou : trapez, tyko przez co będzie przechodził ten trapez ?
2 kwi 20:55
bezendu:
Od kąta pod jakim pada przekrój do płaszczyzny podstawy ?
2 kwi 20:56
zawodus: dobrze, a kiedy jest przypadek graniczny?
tzn, kiedy trójkąt przejdzie w trapez?
2 kwi 21:02
bezendu:
450
2 kwi 21:03
zawodus: zawsze?
2 kwi 21:04
zawodus: czy w naszym zadaniu?
2 kwi 21:04
bezendu:
W zadaniu ?
2 kwi 21:12
zawodus: w zadaniu ok, a jak policzyłeś?
2 kwi 21:15
bezendu:
Na razie to jeszcze nic nie policzyłem.
2 kwi 21:16
zawodus: No właśnie czyli zastanów się jak pokazać, że dla kąta powyżej 45 stopni przekrój będzie
trapezem.
2 kwi 21:24
bezendu:
Ok pomyślę
2 kwi 21:27
Mila:
Zadanie dla bezendu.
Wysokość stożka podzielono na trzy równe odcinki i przez punkty podziału poprowadzono
płaszczyzny równoległe do podstawy. Oblicz stosunek objętości powstałych brył.
2 kwi 21:35
bezendu:
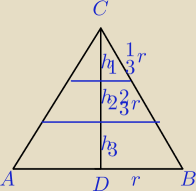
1:7:19
Ja chyba muszę się skupić na planimetrii ?
2 kwi 21:38
bezendu: Dobrze to jest ?
2 kwi 23:31
zawodus: To jest ok.
Wracamy do graniastosłupa
3 kwi 17:35
bezendu:
Dobra, przed chwilą wróciłem z Częstochowy
więc tak długo nie odpisywałem
3 kwi 19:28
pigor: ... , a ja zachęcam maturzystów pobawić się stożkiem
w zadaniu :
Wysokość stożka ma długość H. Miara kąta między wysokością
a tworzącą wynosi 13π. Oblicz pole przekroju płaszczyzną
poprowadzoną przez dwie tworzące wzajemnie prostopadłe.
3 kwi 20:11
muflon: (1/4)H
3(π−2)
3 kwi 20:28
pigor: ... no, niestety nie i nie tylko z powodu tego H
3 
3 kwi 20:43
muflon: wiem wiem, że źle, potreafisz to prawidłowo narysować?
3 kwi 20:51
muflon: ups, a ja policzyłem wg objętość ścinka
3 kwi 20:56
pigor: ... niestety nie potrafię, ale na ...
kartce to tak, dlatego
poczekaj, może inni maturzyści spróbują, w każdym razie mnie
ono zaskoczyło i coś ... znowu nauczyło, może przypomniało,....
3 kwi 21:00
pigor: ... nie, nie bo tym przekrojem jest piękny Δ prostokątny, który, prawda
3 kwi 21:02
pigor: .. a przyszedł do mnie z tym zadaniem przemiły, mądry maturzysta
ze zbiorem zadań III klasa , wyd. OE Pazdro
3 kwi 21:05
muflon: a ile będzie w nim wynosić przeciwprostokatna?
3 kwi 21:15
pigor: ... dziękuję, swoje już powiedziałem , a chyba niepotrzebnie
wciąłem się z tym "prostym" zadankiem ; przepraszam i...znikam, na
godzinkę, a może i mniej/ więcej ...
3 kwi 21:35