nierówność onaa: Zaznacz w układzie współrzednych zbiór wszystkich punktów (x,y) których współrzedne spelniają nierówność y²+x²≤2|x|y Rozbijam to na dwa przypadki gdzie x∊(−∞;0) i gdzie x∊(0;+∞) przerzucam na jedna strone i mam (y−x)²≤0 lub (y+x)²≤0 i nie ma pojęcia jak to dalej

Bogdan: dalej: y = x lub y = −x, to są dwie proste

pomocnik: Kwadrat dowolnej liczby nie może być mniejszy od zera więc może zachodzić tylko równość

pomocnik: Formalnie to dwie półproste

Bogdan: Proste czy półproste?

onaa: czyli ja to pierwiastkuje obustronnie potem czy jak?

Bogdan: Wszystko już zostało napisane: (y − x)² ≤ 0 ⇒ y = x, (y + x)² ≤ 0 ⇒ y = −x,

Bogdan: Są to równania prostych

onaa: dziękuję

pomocnik: Tyle że y=x dla x≤0 a y=−x dla x>0 (więc nie całe proste)

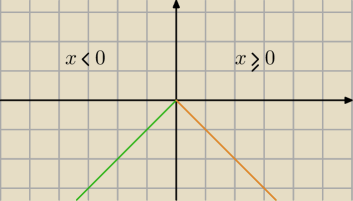
Bogdan: Szkoda, że onna sama nie zauważyła, że w tym zadaniu występują dwie półproste