Analityczna
karlooina:
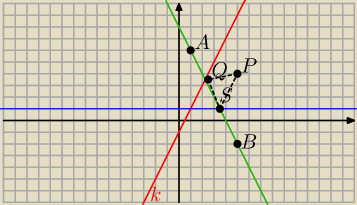
Dana jest prosta k o równaniu y=2x−1, prosta m o równaniu y=1 i punkt P(5,4).
Punkt A ( 1,6 ) jest jest obrazem punktu P w symetrii osiowej względem prostej k.
Punkty B ( 5, −2 ) jest obrazem punktu P w symetrii osiowej względem prostej m.
Q (
94 ,
72 ) i S (
92 , 1 )są punktami przecięcia prostej AB z prostymi k i m
prosta AB : y = − 2x + 8
Wykaż, że spośród wszystkich trójkątów, których jednym z wierzchołków jest punkt P, drugim
wierzchołkiem jest punkt należący do prostej k, a trzecim punkt należący do prostej m,
najmniejszy obwód ma trójkąt PQS .
|PQ| = |QA|
|PS| = |SB|
Czy najmniejszy obwód bedzie w przypadku trójkąta równoramiennego i jeżeli tak to jak to
udowodnić ?
 Dana jest prosta k o równaniu y=2x−1, prosta m o równaniu y=1 i punkt P(5,4).
Punkt A ( 1,6 ) jest jest obrazem punktu P w symetrii osiowej względem prostej k.
Punkty B ( 5, −2 ) jest obrazem punktu P w symetrii osiowej względem prostej m.
Q ( 94 , 72 ) i S ( 92 , 1 )są punktami przecięcia prostej AB z prostymi k i m
prosta AB : y = − 2x + 8
Wykaż, że spośród wszystkich trójkątów, których jednym z wierzchołków jest punkt P, drugim
wierzchołkiem jest punkt należący do prostej k, a trzecim punkt należący do prostej m,
najmniejszy obwód ma trójkąt PQS .
|PQ| = |QA|
|PS| = |SB|
Czy najmniejszy obwód bedzie w przypadku trójkąta równoramiennego i jeżeli tak to jak to
udowodnić ?
Dana jest prosta k o równaniu y=2x−1, prosta m o równaniu y=1 i punkt P(5,4).
Punkt A ( 1,6 ) jest jest obrazem punktu P w symetrii osiowej względem prostej k.
Punkty B ( 5, −2 ) jest obrazem punktu P w symetrii osiowej względem prostej m.
Q ( 94 , 72 ) i S ( 92 , 1 )są punktami przecięcia prostej AB z prostymi k i m
prosta AB : y = − 2x + 8
Wykaż, że spośród wszystkich trójkątów, których jednym z wierzchołków jest punkt P, drugim
wierzchołkiem jest punkt należący do prostej k, a trzecim punkt należący do prostej m,
najmniejszy obwód ma trójkąt PQS .
|PQ| = |QA|
|PS| = |SB|
Czy najmniejszy obwód bedzie w przypadku trójkąta równoramiennego i jeżeli tak to jak to
udowodnić ?