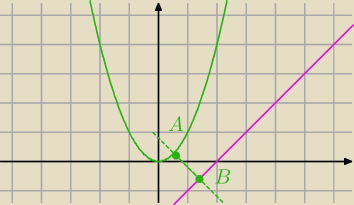
Punkt A leży na paraboli y=x^2, punkt B na prostej x-y=2. Znaleźć długość najkró tony: Punkt A leży na paraboli y=x², punkt B na prostej x−y=2. Znaleźć długość najkrótszego z odcinków AB. Witam! Prosiłbym o pomoc z rozwiązaniem powyższego zadania. Jak to powinno wyglądać? Z góry dziękuję

...:

...: A=(x_A, x_A²) B=(x_B, x_B−2) Prosta zawierająca AB jest prostopadła do y=x−2 ma zatem współczynnik kierunkowy −1 zatem:

	xA2−xB+2
−1=		⇒ −xA+xB=
	xA−xB

tony: A gdyby chcieć to zrobić z pochodnych?

pigor: ... y−y_o= f'(x_o)(x−x_o) równanie stycznej do paraboli y=x² w punkcie na niej A=(x_o,x_o²) || do danej prostej x−y=2 gdzie f(x)=x² i f '(x)= 1 ⇔ 2x=1 ⇔ x_o= ¹₂ , czyli y_o= (¹₂)²= ¹₄ i f' (¹₂)= 2*(¹₂)= 1 , zatem y−¹₄= 1(x−¹₂) ⇔ y= x−¹₄ ⇔ x−y−¹₄=0 równanie stycznej do paraboli równoległej do danej prostej x−y−2=0,

	|−14+2|
więc odległość tych prostych : d=		=
	√1+1

	7
=		=78√2 − szukana odległość. ...
	4√2