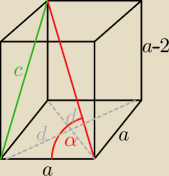
. Tomek: W graniastosłupie prawidłowym czworokątnym wysokość H jest o 2 cm krótsza od krawędzi podstawy a. Pole powierzchni całkowitej tego graniastosłupa wynosi 110 cm². a) Oblicz a i H. b) Zaznacz na rysunku graniastosłupa kąt α nachylenia przekątnej graniastosłupa do ściany bocznej. Oblicz tangens kąta α, a następnie oszacuj, do którego z przedziałów: (0^o, 30^o), (30^o, 45^o), (45^o, 60^o), (60^o, 90^o) należy α.

agulka: a) P_c=2*P_p+4*P_b P_p=a² P_b=a*(a−2) 110=2a²+4a(a−2) 110=2a²+4a²−8a 6a²−8a−110=0 /:2 3a²−4a−55=0 Δ=16+4*3*55=676 √Δ=26

	4−26		−22
a1=		=		, odpada, bo a>0
	6		6

	4+26
a2=		=5
	6

H=a−2=3 b)

	c
tgα=
	a

c²=a²+H² c²=25+9 c²=34 c=2√17

	2√17
tgα=
	5