równanie trygonometryczne z parametrem Zuzia: bardzo proszę o pomoc. wiem, że już się to równanie na tej stronie pojawiło, natomiast rozwiązanie nie było dobre. baaardzo proszę o pomoc, umiem je zrobić tylko do pewnego momentu. mianowicie: dla jakich wartości m równanie sin²x + sinx + m = 0 podstawiłam za sinx t, t ∊<−1,1>, potem Δ≥0 i z tego wychodzi m≤1/4 czyli m ∊ (−∞, 1/4> rozumiem, ze trzeba dodac jeszcze jakies warunki, lecz jakie? skąd w odpowiedziach wynik m∊<−2,1/4> ?

Zuzia: proszę o pomoc

PW:

	1
Dla m∊(−∞,		) istnieją w ogóle rozwiązania, a my chcemy mieć − jak sama napisałaś −
	4

rozwiązania należące do przedziału <−1, 1>. Tak "po chamsku" to muszą być spełnione nierówności

	−1 − √1−4m		−1 + √1−4m		1
−1 ≤		i		≤ 1, m∊(−∞,		).
	2		2		4

52: Dokończ treść pytania...

Zuzia: dokończyłam treść pytania..? PW dziękuję. dlaczego pisałeś 1/4 otwarte? ma być zamknięte prawda? w sensie przedział?

PW:

	1
Tak, to błąd "pisarski" − dla m=		jest Δ = 0 i rozwiązanie istnieje, rozumiesz to
	4

przecież dobrze.

Zuzia: tak, tak, chciałam tylko się upewnić. dzięki raz jeszcze

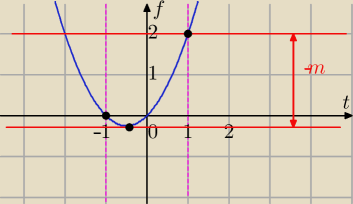
Mila: II sposób dla Zuzi. sin²x+sinx=−m sinx=t , t∊<−1,1> f(t)=t²+t

	−1		−1
tw=		wsp. wierzchołka paraboli,		∊<−1,1> ⇔
	2		2

	−1		1
f(		)=−		wartość najmniejsza f(t) w podanym przedziale
	2		4

Szukamy wartości największej ( na końcach przedziału) f(−1)=0 f(1)=2 wartość największa f(t) w podanym przedziale (2>0)

	−1
zatem		≤−m≤2 /*(−1)⇔
	4

	1
m∊<−2,		>
	4

PW: Mówiłem, że mój sposób nie jest subtelny, ucz się od Mili

Zuzia: dziękuje ślicznie

Mila: Rozwiąż w podobny sposób inne zadanie tego typu.