Logarytmy Qmi: Wyznacz dziedzinę funkcji, logarytmy. f(x) = log_(1−2x) (−x²+x+2) zał: 1−2x>0 −2x > −1

	1
x<
	2

1−2x =/= 1 x =/= 0 −x² + x + 2 > 0 ..... −x²+x+2>0 Δ= 9 , prw z delty = 3 x₁ = 2 x₂ = −1 Zbiór x (−∞, −1) i (2, +∞) Odpowiedź: x∊(−∞,−1)

J: Żle ...

Qmi: tzn?

J: Ostatni warunek: −x² + x +2 > 0

Qmi: No liczymy z tego deltę i x₁ i x₂. Delta wychodzi 9, a x₁ i x₂ się chyba zgadzają.

J: Ale gałęzie paraboli są skierowane ... jak ?

Qmi: na dół

J: No to ... ? Jakie muszą być x ?

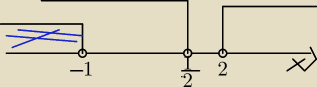
Qmi: Teraz patrze, że powinienem wziąć dodatnie czyli od −1 do 2.

Qmi:

	1
Czyli wynik bedzie x należy do zbioru liczb (−1,		)
	2

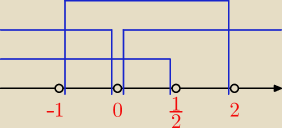
Bogdan: Wykorzystuj możliwości zapisów i sporządzania rysunków tej strony Założenia:

	1
1) 1 − 2x > 0 ⇒ x <
	2

2) 1 − 2x ≠ 1 ⇒ x ≠ 0 3) −x² + x + 2 > 0 ⇒ −(x + 1)(x − 2) > 0 ⇒ x∊(−1, 2)

	1
Część wspólna przedziałów: x∊(−1, 0)∪(0,		)
	2

J:

	1
Dokładnie tak..., podsumujmy: x<		i x ≠ 0 i x ∊ (−1,2) ... określ część wspólną.
	2

J: "Bogdan" .. Daj sie chłopakowi czegoś nauczyć, bo wyraźnie się dzisiaj stara

Qmi: Korzystam, korzystam. Dzięki za pomoc, Muszę być bardziej uważny. Jeszcze raz wielkie dzięki J , Bogdan i Eta

Bogdan: Zamieściłem rozwiązanie tylko dlatego, że chciałem pokazać taki sposób rysowania przedziałów, który nie gubi rozwiązań typu x ≠ 0 oraz wyraźnie pokazuje położenie końców przedziałów.

J: Rozumiem intencje ...., w tym przypadku łatwo było zauważyć,że część wspólna leży wewnątrz przedziału (−1,2) i chciałem, aby to sam zauważył bez rysowania

pigor: ... a więc z definicji logarytmu 1−2x>0 i 1−2x≠1 i −x²+x+2>0 ⇔ 2x<1 i 2x≠0 i x²−x−2<0 ⇔ ⇔ (*) x<¹₂ i x≠0 i x²+x−2x−2<0 ⇒ x(x+1)−2(x+1)<0 ⇔ ⇔ (x+1)(x−2)<0 , stad i z (*) ⇔ −1<x<2 i x<¹₂ i x≠0 ⇔ ⇔ −1< x< 0 v 0< x< ¹₂ ⇔ x∊(−1;0) U (0;¹₂) . ...: