d
Barry: Trójkąt prostokątny ABC, w którym |BCA|=90 i |CAB|=30, jest opisany na okręgu o promieniu
√3. Oblicz odległość wierzchołka C trójkąta od punktu styczności tego okręgu z
przeciwprostokątną.
31 mar 18:33
Janek191:
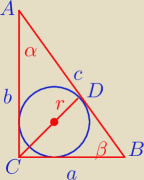
α = 30
o β = 60
o r =
√3
więc
b = a
√3 c = 2 a
Obwód Δ
L = a + b + c = a + a
√3 + 2a = 3a + a
√3 = ( 3 +
√3)*a
Pole Δ
P = 0,5 a*b = 0,5 a* a
√3 = 0,5
√3 a
2 ⇒ 2 P =
√3 a
2
oraz
| | 2 P | |
P = 0,5 L*r ⇒ 2 P = L*r ⇒ |
| = r |
| | L | |
czyli
√3 a = 3
√3 + 3 / :
√3
a = 3 +
√3 ⇒ a
2 = 9 + 6
√3 + 3 = 12 + 6
√3
=========
b = a
√3 = ( 3 +
√3)*
√3 = 3
√3 + 3
==============================
c = 2 a = 6 + 2
√3
===============
Pole Δ
P = 0,5
√3 a
2 = 0,5
√3*( 12 + 6
√3) = 6
√3 + 9
oraz
P = 0,5 c*d ; gdzie d = I CD I
zatem
6
√3 + 9 = 0,5*( 6 + 2
√3)*d
6
√3 + 9 = ( 3 +
√3)*d
| | 6 √3 + 9 | |
d = |
| = 1,5 ( 1 + √3) |
| | 3 + √3 | |
=================================
31 mar 19:41
Barry: dzięki

31 mar 19:44
Eta:

@
Janek ........
to rozwiązanie,które podałeś jest błędne (CD nie przechodzi przez środek okręgu )
Z trójkąta EOB "ekierki" o kątach 30, 60,90
|EO|=r=
√3 to |EB|=DB|=3
|BC|=3+
√3
z tw. kosinusów w trójkącie CDB:
d
2=(3+
√3)
2+3
2−2*3*(3+
√3)*cos60
o ⇒ d
2=....
d=....
31 mar 22:59
Eta:
I jak ?
Janek 
31 mar 23:20
Eta:
Hej
Janek191 
Zaglądałeś tu? ... bo nic nie odpisujesz

1 kwi 12:43
J: Co to znaczy porządny rysunek

1 kwi 12:46
Eta:
A do tego........jak
Barry się cieszy

1 kwi 12:49
J: Albo dalej duma , które rozwiązanie jest dobre

1 kwi 12:51
Eta:
Właśnie dlatego namawiam
Janka by ......

1 kwi 12:52
Janek191:
Czasem można się pomylić

Przepraszam za zamieszanie !
1 kwi 13:14
Janek191:
Mnie wyszło d ≈ 4,098 , a powinno być d ≈ 4,15

1 kwi 13:17
J: 4,01 czy 4,15 ... w sumie róznica niewielka

1 kwi 13:19
pigor: ... no to może na ...

pocieszenie
janka191 mała ...

"szpilka"
w naszą
Etę, a po co z tw. cosinusów (uogólnionego tw. Pitagorasa)
liczyć chcesz, jeśli zauważyłaś, że CD⊥ AB (Δ ekierka ), a więc ...

1 kwi 13:46
pigor: ..., a już na poważnie, to podsumowując jest to dobre zadanie
z punktu widzenia dydaktyki (metodyki) przedmiotu bo na każdy poziom
od gimnazjum po maturę można podać na nie odpowiedni sposób rozwiązania .

1 kwi 13:53
J: Skomplikowany rysunek ... to i obliczenia muszą być skomplikowame

1 kwi 14:05
Eta:
@
pigora "szpilka"

CD nie jest prostopadłe do AB !
1 kwi 19:53
 α = 30o β = 60o r = √3
więc
b = a√3 c = 2 a
Obwód Δ
L = a + b + c = a + a√3 + 2a = 3a + a√3 = ( 3 + √3)*a
Pole Δ
P = 0,5 a*b = 0,5 a* a√3 = 0,5√3 a2 ⇒ 2 P = √3 a2
oraz
α = 30o β = 60o r = √3
więc
b = a√3 c = 2 a
Obwód Δ
L = a + b + c = a + a√3 + 2a = 3a + a√3 = ( 3 + √3)*a
Pole Δ
P = 0,5 a*b = 0,5 a* a√3 = 0,5√3 a2 ⇒ 2 P = √3 a2
oraz

 @Janek ........
to rozwiązanie,które podałeś jest błędne (CD nie przechodzi przez środek okręgu )
Z trójkąta EOB "ekierki" o kątach 30, 60,90
|EO|=r=√3 to |EB|=DB|=3
|BC|=3+√3
z tw. kosinusów w trójkącie CDB:
d2=(3+√3)2+32−2*3*(3+√3)*cos60o ⇒ d2=....
d=....
@Janek ........
to rozwiązanie,które podałeś jest błędne (CD nie przechodzi przez środek okręgu )
Z trójkąta EOB "ekierki" o kątach 30, 60,90
|EO|=r=√3 to |EB|=DB|=3
|BC|=3+√3
z tw. kosinusów w trójkącie CDB:
d2=(3+√3)2+32−2*3*(3+√3)*cos60o ⇒ d2=....
d=....

 Zaglądałeś tu? ... bo nic nie odpisujesz
Zaglądałeś tu? ... bo nic nie odpisujesz




 Przepraszam za zamieszanie !
Przepraszam za zamieszanie !


 pocieszenie janka191 mała ...
pocieszenie janka191 mała ... "szpilka"
w naszą Etę, a po co z tw. cosinusów (uogólnionego tw. Pitagorasa)
liczyć chcesz, jeśli zauważyłaś, że CD⊥ AB (Δ ekierka ), a więc ...
"szpilka"
w naszą Etę, a po co z tw. cosinusów (uogólnionego tw. Pitagorasa)
liczyć chcesz, jeśli zauważyłaś, że CD⊥ AB (Δ ekierka ), a więc ... 


 CD nie jest prostopadłe do AB !
CD nie jest prostopadłe do AB !