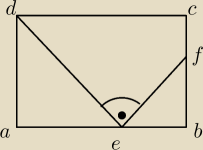
Geometria - pola Krecik: Dwa sąsiednie boki prostokąta ABCD mają długość IABI = 7 oraz IBCI = 3. Z punktu D poprowadzono prostą przecinającą bok AB w punkcie E, a następnie prostą EF tak, że EF prostopadłe do DE i gdzie punkt F należy do BC. Wiedząc, że IDEI = 3*IEFI, oblicz pole czworokąta DEFC. Mógłby ktoś wyjaśnić od czego zacząć lub na co zwrócic uwagę by rozwiązać do zadanie? Pozdrawiam

muflon: Od pola prostokąta odejmij pola 2 trójkątów prostokątnych

Krecik: Tylko jak obliczyć te pola trójkątów? I co teraz? Z pitagorasa wychodzą dwie niewiadome, więc trochę lipa. Może jakoś inaczje oznaczyć boki?

muflon: a układ równań próbowałeś?

muflon: 1 układ pitagoras 2 układ podobieństwo!

muflon: chociaz nie jestem pewnien

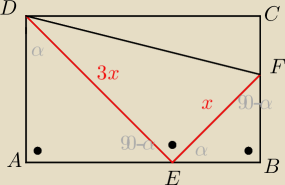
Saizou : i z podobieństwa trójkątów

muflon: oznacz kąty (α. 90−α) w obu trójkątach i ułóż 2 równanie układu z podobieństwa

muflon: o właśnie!

Saizou : ewentualnie można z układu równań z 3 niewiadomymi, ale po co jak z podobieństwa łatwiej i przyjemniej xd

muflon: y=1, x=√5

Krecik: Eh, nie rozumiem tego zadania za bardzo. Wiem o czym mówicie, jednak nie wiem jak to zasotsować w praktyce

muflon: a miałeś układy równań (7−y)²+3²=(3x)² − Pitagoras (3x/x)=3/y − podobieństwo (Tales) masz układ dwóch równań, wyznaczasz x i y, potem podstawiasz pod odpowiednie boki i liczysz pole