l melka: punkty A=(1,−2) C=(4,2) sa dwoma wierzcholkami trojaktya rownobocznego ABC. oblicz wysokosc trojkata

godzio187: pomagam

melka:

godzio187: sorki neta mi odłączyło już przepisuje

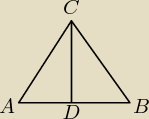godzio187: |CA|=|AB|=|BC| liczymy długość wektora CA √(4−1)²+(2+2)²= √25=5 wiemy że wysokość w równobocznym pada na środek boku AB

	1
czyli AD=AB =		AB=2,5
	2

i teraz z pitagorasa |CA|²=|AD|²+|CD|² √25−6,25=|CD|

√75
	=|CD|
√4

5√3
	=|CD|
2

godzio187:

	a√3
lub poprostu wiemy że h=		tylko w równobocznym gdzie a to nasz bok AB=CA=BC
	2