Dla maturzystów
Domel: DLA MATURZYSTÓW
Zad. 1
Mamy trójkąt prostokątny ABC gdzie ∡BAC = 90°
Z wierzchołka A (5; −7) w kierunku przeciwprostokątnej poprowadzono środkową o dł. 5. Środkowa
leży na prostej k: 3y + 4x + 1 = 0.
Podaj pozostałe wierzchołki trójkąta (wszystkie możliwe) oraz oblicz pole powierzchni trójkąta
31 mar 01:46
Domel:
x wierzchołka B wynosi 6
31 mar 02:19
Domel: 
31 mar 15:23
zombi: Później siądę, chyba że ktoś już zrobi przede mną.
31 mar 15:59
Saizou : czy tych trójkątów jest nieskończenie wiele?
31 mar 16:11
muflon: 2 przypadki
31 mar 17:11
Marcin:
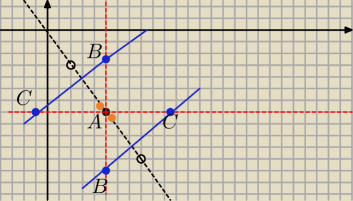
A nie coś takiego?
31 mar 17:12
muflon: gdyby kąt A był dowolny to byłoby nieskończenie wiele przypadków, tak mamy 2, możemy wyznaczyć
2 punkty które są drugimi końcami środkowej( środkami przeciw prostokątnej
31 mar 17:13
muflon: właśnie o tym myślę
31 mar 17:14
muflon: Czy środkowa w tr prostokatnym wychodząca z kąta prostego pokrywa się z dwusieczną?
31 mar 17:15
Marcin:
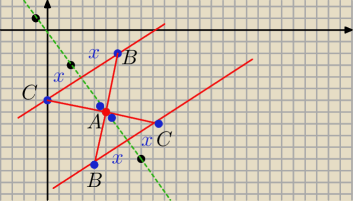
Ale mój rysunek chyba jednak będzie źle.
Bo tak przecież też może być..
31 mar 17:31
muflon: przesuń oś x o 1/3 w górę i będzie okej
31 mar 17:34
muflon: i co nikt nie wiem, może Mila ;>?
31 mar 18:32
Saizou :
przykładowe punkty to :
B(4:−8) C(12:−14)
B(3:−11) C(13:−11)
B(4:−14) C(12:−8)
31 mar 18:48
zombi: Ale napisał Domel, że x wierzchołka B to 6, czyli B(6,yb) czy nie?
31 mar 18:50
Saizou : napisał też że prosi o wszystkie możliwości xd
31 mar 18:53
Sinus: Dla przypadku, że środek przeciwprostokątnej ma współrzędne (2,−3) − B=(6;3/4), C=(−2;−27/4).
Zweryfikuje ktoś? reszty nie chce mi się liczyć...
31 mar 19:04
Saizou : a mi wychodzi że B(6:0)
31 mar 19:21
muflon: Saizou, tylko 1 i 3 para to rozwiązanie, zauważ, że środek odcinka BC dla 2 pary, nie leży na
prostej z treści zadania
31 mar 19:30
zombi: Mi wyszło
C(−2;0) B(6;0)
lub
C(−2−6) B(6−6)
31 mar 19:32
zombi: I jeszcze jeden przypadek dla środku przeciwprostokątnej o współrzędnych (8;−11)
31 mar 19:37
muflon: zombi, te 2 pierwsze przypadki na pewno żle są, odległość środkowej się nie zgadza
31 mar 19:45
Saizou :
punkt (8:−11) leży na prostej 3y+4x+1=0
31 mar 19:45
zombi: No to mamy wygraną środek w (8;−11) i pozostało policzyć dla niego B i C
31 mar 19:46
Sinus: mam błąd w rachunkach, potwierdzam wersje zombiegoXD
31 mar 19:48
zombi: Tak, tylko teraz wystarczy wziąc (8;−11) jako środek i znowu dostaniemy dwie opcje w C i B
31 mar 19:49
muflon: Saizou okej, pomyliłem się, bo uznałem że jedna współrzędna to (−3,−11)
31 mar 19:50
Domel: zombi coś pomieszałeś o 19:32 − prawie dobrze
− ale "prawie" robi różnicę jak z piwem
Żywiec.
No i jeszcze 2 rozwiązania dla twojego przypadku z 19:37.
Ale dobrze kombinujecie − tak trzymać
31 mar 22:51
zombi: Jak bardzo pomieszałem?
bo nie wiem czy metoda zła, czy po prostu rachunki
31 mar 22:59
Domel: Noooo − zamieniłeś punkty C miejscami
31 mar 23:57
Domel: Czyli − połączyłeś trójkąty ? To będzie jakaś nowa figura
1 kwi 00:07
zombi: Aha no tak źle przepisałem.
Dla przypadku, gdy środek środkowej ma współrzędne (2,−3):
C(−2;0) B(6;−6)
lub
C(−2;−6) B(6;0)
Dla przypadku, gdy środek środkowej ma współrzędne (8;−11)
C(10; −11−√21) B(6;−11+√21)
lub
C(10; −11+√21) B(6; −11−√21)
Tak finalnie?
1 kwi 00:43
Domel:
3 kwi 21:37
Saizou : wg mnie jest
∞ tych trójkątów
3 kwi 21:52