plani bezendu: Godzio Pomęczysz trochę planimetrię za mną ?

Godzio: Mogę pomęczyć

bezendu: Dużo tego nie ma 15 zadań. To są takie które robiłem od rana i nie mogę dokończyć.

kyrtap: bezendu do spania

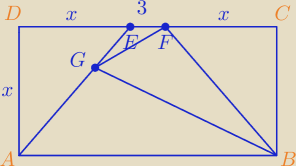
bezendu: 1./ Długości boków prostokąta ABCD spełniają warunki: 2|AD | ≤ |CD | i |CD | = 3 . Na boku CD wybrano punkty E i F w ten sposób, że |DE | = |FC | = |AD | . Punkt G jest takim punktem odcinka AE , że |AG | : |GE | = 2 : 1 . Oblicz długość boku AD prostokąta, dla której pole trójkąta F GB jest największe. Jak zaznaczyć te punkty?

bezendu: @krypt mam na drugą lekcję a moja konkurencja pewnie nie śpi i też robi zadania

kyrtap: konkurencja kogo masz na myśli?

bezendu: Ludzi którzy piszą maturę R i idą na ten sam kierunek. Nie wiesz, że o dostaniu decyduję liczba % z matury ?

kyrtap: wiem wiem

Godzio:

bezendu: Odcinek EF=3−2x ? Odcinek AB=3 I teraz od P_ΔFBG=PABD−te 4 pola małych trójkątów ?

Godzio: Pewnie tak można, ale czy P_FGE się łatwo policzy ?

Godzio: A w sumie tak, bo kąty są ładne. Ta droga będzie ok.

bezendu: A o jakiej jeszcze metodzie myślałeś ?

Godzio: Nie myślałem, nie znalazłem nic prostszego.

bezendu:

	2		9
Liczę to pole i wychodzi −		x(x−		) funkcja kwadratowa więc tego pola nie powinno
	3		4

zapisać się jak funkcji f(x) ? Bo muszę znaleźć wartość największą a takie coś jest dla funkcji ?

Godzio: To pole przedstawia się za pomocą funkcji

	2		3
P(x) = −		x2 +		x
	3		2

I teraz znajdujesz wartość największą. Mam nadzieję, że błędu rachunkowego nie zrobiłeś

bezendu: Chodziło mi o ten właśnie mały szczegół

	9
|AD|=
	8

Godzio: Mi wyszła trochę inna funkcja

bezendu: A jaka ?

Godzio: Ale to już mniejsza o to, dawaj kolejne zadanie, bo wcześnie wstać nie muszę, ale niedługo padnę

Godzio:

	5		3
P(x) = −		x2 +		x
	6		2

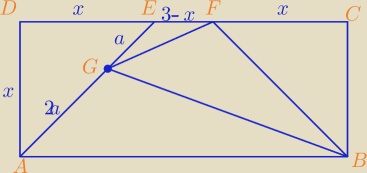
Godzio: Masz do porównania, i tak nic lepszego nie mam do roboty

	x√2
3a = x√2 ⇒ a =
	3

	x2		1		1
PFBG = 3x− (2 *		+		* 2a * 3 * sin(45o) +		a * (3 − x) * sin(135o))
	2		2		2

	x		x		x2
= 3x − (x2 + x +		(3 − x) ) = 3x − x2 − x −		+
	6		2		6

	5		3
P(x) = −		x2 +		x
	6		2

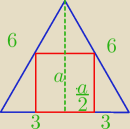
bezendu: 2./ W trójkąt równoboczny o boku długości 6 cm wpisano kwadrat. Oblicz pole tego kwadratu. H−18√3

18√3		3
	=		tak proporcja ?
a		a/2

Godzio: A skąd to 18√3 ?

bezendu: Wysokość trójkąta równobocznego 3√3

Godzio: No Ale to chyba zadanie z podstawy nie ? Proporcja źle ułożona (zobacz, że Ci z niej sprzeczność wyjdzie )

Piotr: jesli mozna : moze by skorzystac z tego ze katy w trojkacie rownobocznym sa rowne 60 ^o ?

Godzio: W tym zadaniu cokolwiek się zrobi będzie dobrze, na pierwszy rzut oka można to zrobić na 3 sposoby

bezendu: To Cię zdziwię bo zadanie z R

3√3		3
	=
3		a   2

bezendu:

3√3		3
	=		teraz jest dobrze
a		a   3−   2

bezendu: Dobra dziękuję, już muszę kończyć

Godzio: Ok