.
Piotr 10: Graniastosłup prawidłowy czworokątny o krawędzi podstawy 6 cm przecięto płaszczyzną
przechodzącą przez środki dwóch sąsiednich krawędzi podstawy. Płaszczyzna ta przecina trzy
krawędzie boczne i jest nachylona do płaszczyzny podstawy pod kątem 600. Zaznacz na rysunku
ten przekrój i oblicz jego pole.
Co to za przekrój będzie? Trapez równoramienny czy nie? I jak ta płaszczyzna może przecinać
trzy krawędzie boczne, jak to rozumieć ?
30 mar 22:46
52:
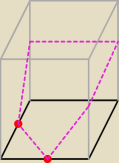
coś takiego chyba
30 mar 22:50
Piotr 10: No właśnie nie wiem, trochę dziwne to pieciokąt wyjdzie ?
30 mar 22:52
52: Tak pięciokąt tylko...
30 mar 22:53
Piotr 10: Ale jak to mozliwe? Jesli to wyjdzie pieciokat, to cały przekroj nie bedzie nachylony do
plaszczyny pod katem 600
30 mar 22:56
52: Przykro mi ale nie pomogę nie umiem...
30 mar 22:56
52: Właśnie zaczynam się zastanawiać nad tym nachyleniem, ale innej opcji nie ma...
30 mar 22:57
Piotr 10: No wlasnie tez sie mecze z tym

ale to troszke dziwne ,
30 mar 22:58
52: Masz odp do tego ?
30 mar 23:01
Piotr 10: Właśnie szukam klucza do arkusza, może uda sie znaleźć do podesle
30 mar 23:04
Saizou: zadanie z nowej ery ?
30 mar 23:05
Piotr 10: Niee z maturki z Bydgoszczy
30 mar 23:06
Piotr 10: 52 tak to będzie pieciokat foremny
P=63 cm2
30 mar 23:07
Piotr 10: bez tego slowa ''foremny'' nie wiem czemu to wpisalem

30 mar 23:08
52: Mi wyszło 108 ale to takie obliczenia po mojemu

30 mar 23:08
Marcin: To będzie trapez równoramienny i trójkąt równoramienny

30 mar 23:08
Saizou: takie samo, albo bardzo podobne jest w nowej erze, jak chcesz to jutro moge ci wrzucic schemat
oceniania. a pieciokat to dobra wersja xd
30 mar 23:09
Piotr 10: Saizou juz znalazlem klucz

30 mar 23:09
Marcin:
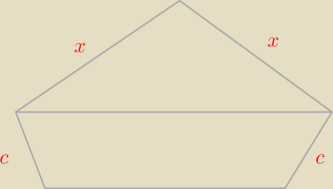
30 mar 23:10
Piotr 10: pierwszy raz sie spotkalem ze przekrojem w brylach jest pieciokąt , ale dobra xd
30 mar 23:10
Marcin: Ja jak mam robić przekrój, to zawsze patrzę się na swój pokój i sobie to próbuję wyobrazić,
polecam

30 mar 23:11
Piotr 10: Jak mam te zadanie dalej ruszyć ?
30 mar 23:26
Marcin: | | 3 | |
Znasz kąt nachylenia tego przekroju, a jeden z boków (ten z podstawy ma |
| krawędzi |
| | 4 | |
podstawy.
30 mar 23:33
Marcin:
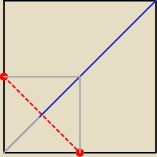
Oczywiście nie krawędzi podstawy, tylko przekątnej podstawy,
30 mar 23:35
Piotr 10: nie wiem co mam liczyc kompletnie
30 mar 23:41
Piotr 10: Dobra idę coś poczytać, bo nie myśle już, dzięki za pomoc

30 mar 23:43
Marcin: Jutro wymyślisz

Dobrej nocy

30 mar 23:44
Mila:
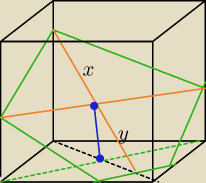
Podpowiedź.
31 mar 14:48
Piotr 10: ok zaraz sie biore za to
31 mar 15:01
Saizou :
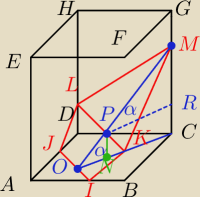
w nowej erze, jest bardzo podobne zadanko
Graniastosłup prawidłowy czworokątny o krawędzi podstawy a przecięto płaszczyzną przechodzącą
przez środki dwóch sąsiednich krawędzi podstawy. Płaszczyzna ta przecina trzy krawędzie boczne
i jest nachylona do płaszczyzny pod kątem α. Oblicz pole otrzymanego przekroju?
wrzucić pół alfabetu xd
P=?
| | (IJ+KL)*OP | | 1 | |
P=Ptrap+Ptrój= |
| + |
| KL*MP |
| | 2 | | 2 | |
lMPl to wysokość trójkąta KLM
| | 1 | | a√2 | | a2 | |
Ptrój= |
| *a√2* |
| = |
| |
| | 2 | | 2cosα | | 2cosα | |
| | 1 | | a√2 | | a√2 | |
Ptrap= |
| ( |
| +a√2)* |
| |
| | 2 | | 2 | | 4cosα | |
w twoim zadaniu a=6 a α=60 czyli
31 mar 15:30
kyrtap: Łapcie matematycy
Wszystkie krawędzie prawidłowego ostrosłupa czworokątnego mają długość a. Oblicz pole przekroju
płaszczyzną poprowadzoną przez środku dwóch sąsiednich krawędzi podstawy i środek wysokości
ostrosłupa.
31 mar 15:50
zawodus: było w necie tyle razy...
31 mar 15:52
kyrtap: myślałem że chce ktoś rozwiązać
31 mar 16:28
Piotr 10: Saizou ja to troszkę inaczej ( chyba ) zrobiłem zaraz zobacze Twój sposob
31 mar 18:37
Saizou : tylko u mnie na literkach, bo takie było zadanko xd
31 mar 18:49
Piotr 10: Taki sam wynik otrzymałem, trochę trudne zadanie ( jak dla mnie oczywiscie ) , dzięki

31 mar 18:53
Saizou : trzeba mieć po prostu pomysł i tyle

i nie robić błędów rachunkowych takich jak ja xd
31 mar 18:54
Piotr 10: No na próbnej maturce, sprawdzałem sobie zadania i jedno miałem później poprawic, bo
wiedzialem ze mam tam blad w minusach i zapomnialem w koncu o tym i wyszedlem z klasy mimo,
ze mialem jesszcze z 40 minut xD
31 mar 18:56
Saizou : życie ....

ja ostatnio nie doczytałem że co najmniej 4 osoby

31 mar 18:58
Marcin: Można sobie 'załatwić' takie zaświadczenie, że jeżeli masz dobry sposób rozwiązania, ale mylisz
się w samych obliczeniach, to i tak masz pełną ilość punktów za zadanie

31 mar 18:59
Saizou : haha a po co? wystarczy skupić się na 60% na maturze i będzie dobrze xd
31 mar 19:00
Marcin: Niektórych zjada stres

31 mar 19:01
Piotr 10: Ja na probnej robiona przez moja szkola z poziomu roz stracilem jeden punkt wlasnie w znakach w
minusach

zadanie dotyczlo wielomianu z wykorzystaniem III stopnia wzorow Viete'a , cos w
stylu
suma kwadratow pierwiastkow wielomianu W(x)=ax
3+..... jest rowna 14
31 mar 19:02
Saizou : keep calm and pass the best of matura exam

31 mar 19:03
kyrtap: przyznam stres robi swoje
31 mar 20:45
 coś takiego chyba
coś takiego chyba
 ale to troszke dziwne ,
ale to troszke dziwne ,






 Oczywiście nie krawędzi podstawy, tylko przekątnej podstawy,
Oczywiście nie krawędzi podstawy, tylko przekątnej podstawy,

 Dobrej nocy
Dobrej nocy 
 Podpowiedź.
Podpowiedź.
 w nowej erze, jest bardzo podobne zadanko
Graniastosłup prawidłowy czworokątny o krawędzi podstawy a przecięto płaszczyzną przechodzącą
przez środki dwóch sąsiednich krawędzi podstawy. Płaszczyzna ta przecina trzy krawędzie boczne
i jest nachylona do płaszczyzny pod kątem α. Oblicz pole otrzymanego przekroju?
wrzucić pół alfabetu xd
P=?
w nowej erze, jest bardzo podobne zadanko
Graniastosłup prawidłowy czworokątny o krawędzi podstawy a przecięto płaszczyzną przechodzącą
przez środki dwóch sąsiednich krawędzi podstawy. Płaszczyzna ta przecina trzy krawędzie boczne
i jest nachylona do płaszczyzny pod kątem α. Oblicz pole otrzymanego przekroju?
wrzucić pół alfabetu xd
P=?

 i nie robić błędów rachunkowych takich jak ja xd
i nie robić błędów rachunkowych takich jak ja xd
 ja ostatnio nie doczytałem że co najmniej 4 osoby
ja ostatnio nie doczytałem że co najmniej 4 osoby 


 zadanie dotyczlo wielomianu z wykorzystaniem III stopnia wzorow Viete'a , cos w
stylu
suma kwadratow pierwiastkow wielomianu W(x)=ax3+..... jest rowna 14
zadanie dotyczlo wielomianu z wykorzystaniem III stopnia wzorow Viete'a , cos w
stylu
suma kwadratow pierwiastkow wielomianu W(x)=ax3+..... jest rowna 14
