analityczna komik: Przyprostokatna AB trójka˛ta prostokatnego ABC jest zawarta w prostej o równaniu 2y + x + 6 = 0, a srodek jego przeciwprostokatnej BC ma współrzedne S = (9, 0). Oblicz współrzedne wierzchołka C jezeli cos∡ACB = 3√10/10 . od czego zacząć ?

zombi: Btw. ma ktoś odpowiedzi do tej maturki dzisiejszej ?

komik: właśnie. przydały by się. A ma ktoś pomysł jak zrobić to ?

zombi: Ja mam, ale analitycznej nigdy nie jestem pewien, więc powiem, dopiero gdy ktoś poda odpowiedzi

komik: ale chociaż o czego zacząłeś, co wyznaczyłeś i jak ten cosinus wykożystać

komik: ?

zombi: Już ci rozpisuję

komik: dzięki

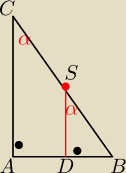
zombi: Dane: AB: 2y+x+6=0 S(9,0)

	3√10		3
cos∡ACB =		=
	10		√10

1. Odcinki |SC| = |SB| 2. Szukam prostej SD (SD⊥AB oraz przechodzi przez S) 3. Przyrównuję prostą SD z AB i otrzymuje współrzędne punktu D 4. Trójkąty ABC oraz DBS są ~ z cechy (kk) wobec tego ∡ACB = ∡DSB 5. Liczę długość długość SD

	|SD|
6. cosα =
	|SB|

7. otrzymuję dlugość SB skąd mam już punkt B (dwie możliwości) 8. prosto z jednokładności czy wektorków otrzymujesz C

komik: dzięki wielkie. rozumiem wszystko oprócz tego jak otrzymujesz punkt B mógłbyś wytłumaczyć?

Marcin: Masz |SD| i masz |SB|. Wiesz że ΔDBS jest prostokątny. także nie powinno być problemów

komik: mam zaćmienie dalej nie wiem. jak punkt z długości obliczyć ?

zombi:

	1
Punkt B ma współrzędne (x, −		x−3) jeśli dobrze pamiętam znasz |SB| więc
	2

√(9−x)² + (0−(−¹₂x−3))² = |SB| − a tu mamy naszą wartość, zwyczajna kwadratówka dwa

	1
rozwiązania będą. To −		x−3 pisałem na oko z pamięci bo nie mam kartki obok.
	2

Marcin: |DS|²+|DB|²=|SB|² Współrzędne D i S znasz, a B należy do prostej AB

komik: rzeczywiście wcześniej napisałeś <otrzymuję dlugość SB skąd mam już punkt B> jakby to miało być takie oczywiste i banalne. Dlatego nie siągnąłem do tego że punkt b leży na prostej AB i ma takie współzedne. dzięki za pomoc

zombi: Sorka za skrót myślowy

komik: