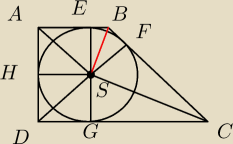
okrąg wpisany w trapez prostokątny, odległości środka okręgu od wierzchołków Adr: Długość dłuższej podstawy trapezu prostokątnego wynosi 17. Oblicz odległości środka okręgu o średnicy 10, wpisanego w ten trapez od jego wierzchołków. Mam problem z obliczeniem jednego z tych odcinków. A dokładnie z odcinkiem SB. Resztę mam obliczoną. AS=DS= 5√2 SC=13 Pomoże ktoś?

wredulus: zauważ, że: DG = r ... w takim razie znasz GC FC = GC (trójkąty przystające) BF = BC − FC znasz BF ... znasz 'r' wyliczasz BS z trójkąt prostokątnego lub krócej ale 'na to samo kopyto': EB = AB − AE = AB − r znasz EB, znasz r ... trójkąt prostokątnych i masz BS

wredulus: ajjj .. .Ty znasz tylko dolną podstawę ... no to 'pierwszy wariant' robisz

Adr: ale nie wiem ile wynosi BC

Eta: |FB|=17−5=12 z podobieństwa trójkątów BOE i OEC z cechy (kkk)

r		12
	=		⇒ x=....
x		r

i dwa razy z tw. Pitagorasa : |OC|=√r²+x²=..... , |OB|=√5²+12²=.... i po bólu

wredulus:

	12
sin(∡GSC) =
	13

	12		FS
cos(∡FSB) = cos(90o − ∡GSC) = sin(∡GSC) =		=
	13		BS

i stąd masz |BS|