liczba kombinacji w układzie kartezjanskim robak15: Na ile sposobów można z punktu (0, 0) w układzie kartezjańskim dotrzeć do punktu (7, 10), jeśli można poruszać się tylko w prawo i do góry. W prawo można poruszać się tylko o 1, 2 lub 4 jednostki, a w górę można poruszać się tylko o 1, 2, 3 lub 4 jednostki. Proszę o pomoc

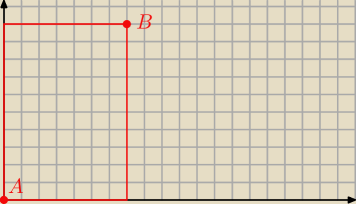
wredulus: zauważ, że aby dojść z A do B musisz wykonać dokładnie 7+10 = 17 ruchów (bo można tylko w prawo i do góry) ... z czego 7 ruchów będzie w prawo ... a 10 do góry Więc pytanie brzmi: Na ile sposób można rozmieścić 7 'w prawo' na 17 miejscach na ruchy

robak15: Dodatkowe założenie jest takie, że poruszamy się raz w lewo raz w górę na przemian.

wredulus: hę jak w lewo

wredulus: ojjj ... nie doczytałem do końca to jest warunek dodatkowy

robak15: raz w prawo a raz w góre

wredulus: skoro 'w prawo' można się poruszać o 1,2 lub 4 krechy (a w sumie musisz się poruszyć o 7) to masz możliwości: I) 1,1,1,1,1,1,1 II) 1,2,2,2 III) 1,2,4 i tyle skoro mają być 'na przemian' do dla (I) ruchów do góry może być albo 8 albo 6 stąd: I.a) 1,1,1,1,1,1,1,3 I.b) 1,1,1,1,2,4 I.c) 1,1,1,1,3,3 a dla (II) mamy liczbę ruchów 'do góry' 3 lub 5: II.a) 1,1,1,3,4 II.b) 1,1,2,3,3 II.c) 1,1,2,2,4 II.d) 1,2,2,2,3 II.e) 2,2,2,2,2 II. f) 2,4,4 II.g) 3,3,4 a dla (III) mamy liczbę ruchów 'do góry' 2 lub 4: III.a) 1,1,4,4 III.b) 1,2,3,4 III.c) 2,2,2,4 III.d) 1,3,3,3 III.e) 2,2,3,3 i tyle (w 2 ruchach 'do góry' się nie dojdzie) no i oczywiście wszelkie 'kombinacje' "pozycjonowania" danych ruchów trochę roboty z tym jest

robak15: nie chodzi o rozpisanie, ale o obliczenia kombinatoryczne, bo tak to mam obliczyć

wredulus: no to Ci rozpisałem jakie obliczenia masz przeprowadzić