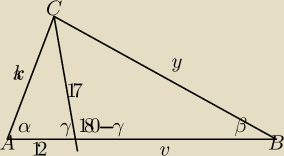
 Dany jest trójkąt ABC, w którym SinA/SinB=17/25. Na boku AB leży punkt D taki, że AD=12 i
DB=16, oraz CD=17 . Oblicz długość promienia okręgu opisanego na trójkącie
∫x=17y/25
∫x2=122+172−408cosγ
∫y2=172+162−544cos180−γ
czy to jest dobrze? jeśli tak to czy ktoś umiałby to ktoś rozwiązać? mi to nie wychodzi wgl
dziękuję
(naprzeciwko γ jest x)
Dany jest trójkąt ABC, w którym SinA/SinB=17/25. Na boku AB leży punkt D taki, że AD=12 i
DB=16, oraz CD=17 . Oblicz długość promienia okręgu opisanego na trójkącie
∫x=17y/25
∫x2=122+172−408cosγ
∫y2=172+162−544cos180−γ
czy to jest dobrze? jeśli tak to czy ktoś umiałby to ktoś rozwiązać? mi to nie wychodzi wgl
dziękuję
(naprzeciwko γ jest x)

| sina | 17 | ||
= | |||
| sinb | 25 |
