.
bezendu:
Bryły.
30 mar 17:59
Saizou : tak

30 mar 18:03
bezendu: Nie jesteś w temacie

30 mar 18:03
Eta:
Ciekawe zadanie ....

30 mar 18:04
bezendu: Mila kazała założyć temat bo ma do mnie dwa zadania.
30 mar 18:05
Saizou : jak nie jestem? a kogo jest 2 post

30 mar 18:06
Mila: 1)
Podstawą ostrosłupa jest prostokąt o bokach 9cm i 12 cm; krawędzie boczne mają po 12,5 cm.
Oblicz objetość tego ostrosłupa.
2)
Podstawą ostrosłupa jest trójkąt równoramienny o ramieniu długości 6cm i podstawie długości
8cm. Krawędzie boczne są równe i mają po 9 cm długości.Oblicz objetość tego ostrosłupa.
3)
Podstawą ostrosłupa jest trójkąt równoramienny o ramieniu długości 39cm i podstawie długości
| | π | |
30cm. Każda ze ścian bocznych tworzy z płaszczyzną podstawy kąt α= |
| . |
| | 4 | |
Oblicz objętość ostrosłupa.
30 mar 18:09
bezendu:
1. To miałem na sprawdzianie to wynik mogę od razu podać
V=360cm
3 i to było zadanie z podstawy

30 mar 18:12
bezendu:
2. Pole trójkąta równoramiennego.
h
Δ=6
2−4
2=20
h=2
√5
P
Δ=8
√5
Z tw Pitagorasa mam:
V=48cm
3
30 mar 18:21
bezendu: 3.
h
Δ=36
P
Δ=540cm
2
R−Promień okręgu opisanego na trójkącie
V=3802,5cm
3
30 mar 18:27
bezendu:
Takie zadania to nie problem i raczej daleko im z poziomem do tego co jest w maju na R. Ja
zaraz wstawię zadania z którym mam kłopot.
30 mar 18:30
Mila:
3 zadanie źle.
Spodek wysokości leży w środku okręgo wpisanego w podstawę.
Zauważ różnicę w treści w stosunku do 1 i 2 zadania. To ważne!
30 mar 18:31
bezendu:
korekta V=1800cm3
30 mar 18:39
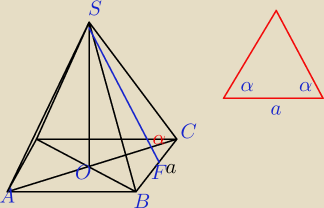
bezendu:
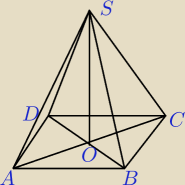
Dany jest ostrosłup prawidłowy czworokątny ABCDS o podstawie ABCD . W trójkącie równoramiennym
ASC stosunek długości podstawy do długości ramienia jest równy |AC | : |AS | = 6 : 5 . Oblicz
sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
30 mar 18:43
Mila:
wskazówka:
x− wspólna miara
|AC|=6x
|AS|=5x
oblicz wszystko co potrzebne w zależności od x, potem Ci się uprości.
30 mar 18:58
30 mar 19:13
Mila:
Wynik dobry.
30 mar 19:44
30 mar 19:45
bezendu:
Nawet nie przeglądałem tych zadań na matematyka.pisz dotyczących brył.
30 mar 19:47
Piotr 10: Zerknij na mój post

30 mar 19:54
bezendu:
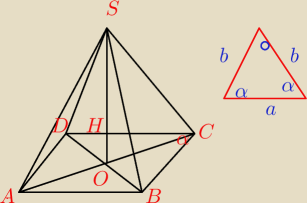
W ostrosłupie prawidłowym czworokątnym dane są: H – wysokość ostrosłupa oraz α — miara kąta
utworzonego przez krawędź boczną i krawędź podstawy (45
∘ < α < 90
∘).
| | 4 | | H3 | |
Wykaż, że objętość V tego ostrosłupa jest równa |
| * |
| |
| | 3 | | tg2α−1 | |
bsin2α=asinα
a=2bcosα
P
p=4b
2cos
α
I dalej bez sensu już zupełnie

Jak uzależnić wszystko od H ?
Jak by kąt α był międy krawędzią boczną a płaszczyzną podstawy to nie miałbym pytań

30 mar 20:04
zawodus: napisz mi jak chcesz dojść do policzenia wysokości?
w ostrosłupach są 2 trójkąty charakterystyczne

30 mar 20:05
bezendu:
Ja mam daną wysokość właśnie. Fajnie by było jak bym jej nie miał podanej. Wysokość w zadaniu
jest dana H
30 mar 20:07
zawodus: źle przeczytałem

wskazówka:
wykorzystaj trójkąt utworzony przez wysokość, wysokość ściany bocznej i połowę podstawy.
30 mar 20:11
bezendu:
liczyłem tak ale też nic nie wychodzi
30 mar 20:13
zawodus: to pokaż jak liczysz, bo wychodzi

30 mar 20:13
bezendu:
obliczyłem wysokość ściany bocznej bsinα połowa boku ma bcosα
30 mar 20:14
zawodus: zauważ, że b ci nie potrzebne do niczego

potrzebujesz długości podstawy, powiedzmy a.
Teraz liczymy wysokość ściany bocznej
30 mar 20:16
bezendu:
Uzależniłem a od b
a=2bcosα wyżej masz obliczenia.
30 mar 20:18
zawodus:
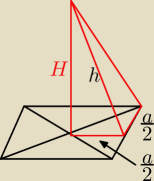
chodziło mi o coś takiego.
30 mar 20:23
Mila:
h
b− wysokość ściany bocznej.
W ΔSMC, M środek BC
oblicz z tego a
2 i gotowe.
30 mar 20:23
bezendu:
Nie mam danej ani h ani a. Skąd mam na to wpaść ?
30 mar 20:26
zawodus: Mila ci już podała co dalej.
30 mar 20:28
bezendu:
Tylko, że tego wgl nie rozumiem.
30 mar 20:30
zawodus:
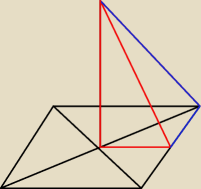
najpierw z niebieskiego wysokość ściany bocznej potem czerwony i Pitagoras
dlaczego? w niebieskim jest α, a w czerwonym H − twoje wszystkie dane
30 mar 20:33
bezendu:
z niebieskiego wysokość ściany bocznej
30 mar 20:38
zawodus: h i a to przyprostokątne to skąd sinus?

30 mar 20:49
bezendu:
s twierdzenia sinusów skoro mam kąt α
30 mar 20:50
zawodus: twierdzenie sinusów powinno być tak:
30 mar 20:53
bezendu:
Ale wtopa

30 mar 20:56
Mila:
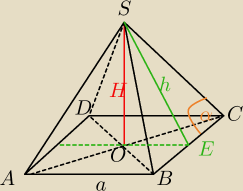
W ΔSEC:
W ΔSOE: z tw. Pana Pitagorasa:
| | 1 | | 1 | |
( |
| a*tgα)2=H2+( |
| a)2⇔ |
| | 2 | | 2 | |
a
2*(tg
2α−1)=4H
2
30 mar 20:58
bezendu:
A ze sposobu zawodusa. ? Nie widziałem, że nie mając danych tak można. Ja chciałem na zmiennych
a i b ale się nie udało .
30 mar 20:59
zawodus: koniec i kropka.
30 mar 21:00
zawodus: to jest ten sam sposób co ja

30 mar 21:02
Mila:
U ZAwodusa jest to samo.
Nie czytasz tego, co Ci piszę. Już Ci w poprzednim zadaniu pisałam, że się skracają niewiadome,
ale Ty uparcie to omijasz.
Słowo pisane trzeba analizować, za chwilę będziesz studiował i musisz czytać teksty
matematyczne i nie tylko, ze zrozumieniem.
30 mar 21:04
bezendu: Czytam, poprzednie zadanie zrobiłem przecież. Ty liczysz z tg a ja się pytam o twierdzenie
sinusów.
30 mar 21:10
zawodus: Ale dostajesz dokładnie to samo.
u ciebie
u
Mili
widzisz różnicę?

30 mar 21:12
Mila:
Nie widziałam Twojego wpisu 20: 56, bo go nie było gdy pisałam rozwiązanie.. Kolega Ci już
odpowiedział.
30 mar 21:20
bezendu: To jest to samo. Dobra przepraszam za zamieszanie. Tylko szkoda, że ja tego nie widziałem
30 mar 21:23
Kermi:): bezendu bardzo często Cie tu widuje,piszesz mature rozszerzona w tym roku czy robisz to 4fun ;
)?
30 mar 21:28
bezendu:
4fun

30 mar 21:29
Kermi:): przyznam,masz łeb jak sklep

Pozdrawiam!
30 mar 21:30
bezendu:
A tak na poważnie to nie dla 4fun

tylko pierwsza opcja a czemu pytasz ?
30 mar 21:31
Kermi:): Jestem ciekawy gdzie celujesz
30 mar 21:33
bezendu: Powiem tylko, że PWr jak się uda, reszta to tajemnica.
30 mar 21:33
Kermi:): =]
Wracam do trygonometri. bless!
30 mar 21:35
bezendu: 
30 mar 21:37
bezendu:
Mila masz jakieś zadanie podobne do tego w którym jest podany właśnie kąt między kr.
boczną a krawędzią podstawy i nie ma danych tylko literki ?
30 mar 22:34
Mila:
4)
Dlugość wysokości ostrosłupa prawidłowego trójkatnego jest równa długości krawędzi podstawy,
wyznacz miarę kąta między krawędzią boczną a płaszyzną podstawy.
5) W ostrosłupie prawidlowym czworokątnym, krawędź podstawy ma dl. a, natomiast kat między
krawędzią boczną i krawedzią podstawy wychodzącą z tego samegowierzcholka ma miarę α.
Oblicz objętość i pole powierzchnicałkowitej ostrosłupa.
30 mar 22:44
bezendu:
1. α=3√3 ?
30 mar 22:50
Mila:
W (1) miara kata!
30 mar 22:54
bezendu:
Nie skróciłem α=√3 α=600 ?
30 mar 22:55
Mila:
tgα=√3⇔α=60o
30 mar 23:06
bezendu:
2hctgα=a
H=U{2a
√1−ctg2α{4ctgα}
Ok jak do tej pory ?
30 mar 23:07
bezendu: ?
30 mar 23:43
bezendu: ?
31 mar 00:00
Mila:
Wygląda dobrze, ale zapisałabym h, tak
wtedy masz łatwiejsze rachunki.
| | a | |
H= |
| √tg2α−1 zbadaj kiedy tg2α−1>0 |
| | 2 | |
Dobranoc, dokończ, jutro sprawdzę.
31 mar 00:07
bezendu:
Dobranoc. Dziękuję.
31 mar 00:09
bezendu:
Ale czemu ma rozwiązać tę nierówność
(tgα−1)(tgα+1)>0 ?
31 mar 18:42
Mila:
Badasz dla jakiego α wyrażenie pod pierwiastkiem jest nieujemne .
Jeśli kąt mniejszy od 45o to pod pierwiatkiem będzie liczba ujemna, a tak nie może być.
31 mar 18:56
bezendu: OK a dalej co mam robić. ?
31 mar 19:00
31 mar 19:34
Mila:
V dobrze, jeszcze P
c.
31 mar 19:55
bezendu:
Pc=a2(1+tgα) ?
Te zadania już były na poziom R czy jeszcze za proste ?
31 mar 20:04
zawodus: Wg mnie 4 za łatwe a 5 na rozszerzenie pasuje.
31 mar 20:13
Mila:
5R
31 mar 20:17
bezendu: To poszukam teraz jakiś przekroi bo tego też jeszcze nie do końca rozumiem.
31 mar 20:18
zawodus: Wg mnie "przekrojów"

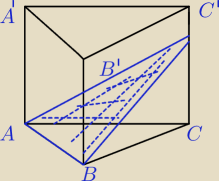
Coś prostego.
Dany jest graniastosłup prawidłowy trójkątny o krawędzi podstawy równej 2
√3 i wykości równej
3. Graniastosłup ten przecięto płaszczyzną zawierającą krawędź podstawy i nachyloną do
płaszczyzny podstawy pod kątem 30 stopni. Obliczu pole otrzymanego przekroju.
31 mar 20:38
bezendu:
31 mar 20:43
Mila:
No i co? Są problemy? Dlaczego nie jest zaznaczony kąt?
Najpierw zbadaj, czy przekrój jest trójkątem, czy trapezem.
31 mar 20:58
bezendu:
Chodzi o ten przekrój ? Już zabieram się do liczenia.
31 mar 21:11
bezendu:
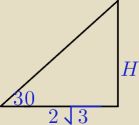
2H=6
H=3
krawędź BE=
√21
Przekrój jest trójkątem.
31 mar 21:25
Damian: Może to spróbujesz policzyć bo nie mogę nic wykombinować

Wewnątrz kąta o mierze 60
0 znajduje się punkt A odległy od jednego z ramion o 3 a od drugiego
o 6. Oblicz odległość punktu A od wierzchołka kąta.
31 mar 21:29
Damian:
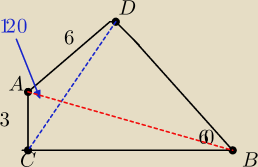
0
31 mar 21:32
Damian: z tw.cos obliczyłem CD = √63
31 mar 21:34
Damian: zapisałem długość boku CB= a i BD=b i z tw. cos dla ΔCBD a potem zapisać a od b korzystając z
tego że ΔACB i Δ ABD są prostokątne ale coś nie za bardzo wychodzi
31 mar 21:37
zawodus: Bezendu ale wysokość miałeś podaną
31 mar 21:39
bezendu:
@Damian zaraz policzę

31 mar 21:44
zawodus: Zadanie z graniastosłupem nadal czeka. Twoje wytłumaczenie jak na razie kompletnie
niezrozumiałe

31 mar 21:48
bezendu:
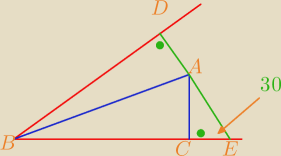
For Damian.
|AE|=6
|CE|
2=6
2−3
2
|CE|
2=27
|CE|=3
√3
|BE|=8
√3
|BC|=|BE|−|CE|
|BC|=5
√3
|AB|
2=3
2+(5
√3)
2
|AB|
2=84
|AB|=2
√21
31 mar 21:50
Mila:
Damianku, załóż nowy wątek dla siebie, to tam Ci pomożemy.
31 mar 21:50
zawodus: Mila zadanie z głowy, a specjalnie nie podałem, że to trójkąt.

31 mar 21:52
bezendu:
|EF|=3√2
P=3√6 ?
31 mar 21:54
bezendu:
No i co tak milczysz Damian ? Masz rozwiązanie od A do Z ?
31 mar 21:55
Damian: dzięki zaraz to przeanalizuję

odp. jest dobra
31 mar 22:01
bezendu:
To dobrze bo planimetria to nie mój klimat.
31 mar 22:02
Damian: Wszystko jasne

ja od razu zły trop obrałem

31 mar 22:05
bezendu:
Dobrze mi wyszło z tym przekrojem ?
31 mar 22:05
Mila:
Zawodus, przepraszam, nie zauważyłam, że to Twoje zadanko, ( bardzo dobry pomysł),
myslałam , że
bezendu podał i czeka na pomoc.

31 mar 22:10
bezendu:
A dobrze wyszło ?
31 mar 22:13
Mila:
Widzę, że Zawodusa obraziłam i wycofał się.
Wg mnie źle policzyłeś.
31 mar 22:53
bezendu:
Zaowdus się nie obraził, na pewno się uczy

Jeszcze źle ?
31 mar 22:55
Mila:
Jaka jest wysokość w podstawie?
31 mar 22:57
bezendu:
Czemu usunęłaś swój post ?
Tam był h=3
31 mar 23:01
Mila:
Dalej, jak liczyłeś wysokość przekroju.
31 mar 23:10
bezendu:
z tw pitagorasa hp=32+32
31 mar 23:15
Mila:
A dlaczego tak?
31 mar 23:19
bezendu:
A to nie jest trójkąt prostokątny ? Wrócę jutro do tego bo dziś muszę jeszcze napisać pracę
maturalną. Dziękuję za pomoc. Dobranoc.
31 mar 23:21
Mila:
Dobranoc, narysuj jutro rysunek z oznaczeniami.

31 mar 23:32
zawodus: Mnie się nie da obrazić

(chyba

).
Po prostu musiałem iść

Dziękuję
Mila za kontynuację problemu

1 kwi 08:57
zawodus: Niestety, ale z moich małych rachunków nie wychodzi takie pole.
1 kwi 08:58
bezendu:
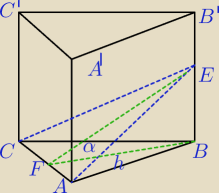
h=3
√3|FE|=6
|FE|=2
√3
EB=
√3
Więc pole P=0,5*
√3*2
√3=3 ?
1 kwi 17:12
Mila:
Masz obliczyć pole ΔACE:
1 kwi 17:18
bezendu: =6
1 kwi 17:26
Mila: Dobrze.
1 kwi 17:34
bezendu:
Po 19 wstawię dwa zadania problematyczne.
1 kwi 17:40
zawodus: To teraz trudniejsza wersja tego zadania. Treść ta sama tylko zmiana kąta nachylenia z 30
stopni na 60.
1 kwi 21:37
bezendu:
FE=6
P=0,5*2
√3*6=6
√3
1 kwi 21:40
Mila:
Załóżcie nowy wątek.
1 kwi 22:08





 Dany jest ostrosłup prawidłowy czworokątny ABCDS o podstawie ABCD . W trójkącie równoramiennym
ASC stosunek długości podstawy do długości ramienia jest równy |AC | : |AS | = 6 : 5 . Oblicz
sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.
Dany jest ostrosłup prawidłowy czworokątny ABCDS o podstawie ABCD . W trójkącie równoramiennym
ASC stosunek długości podstawy do długości ramienia jest równy |AC | : |AS | = 6 : 5 . Oblicz
sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy.

 W ostrosłupie prawidłowym czworokątnym dane są: H – wysokość ostrosłupa oraz α — miara kąta
utworzonego przez krawędź boczną i krawędź podstawy (45∘ < α < 90∘).
W ostrosłupie prawidłowym czworokątnym dane są: H – wysokość ostrosłupa oraz α — miara kąta
utworzonego przez krawędź boczną i krawędź podstawy (45∘ < α < 90∘).
 Jak uzależnić wszystko od H ?
Jak by kąt α był międy krawędzią boczną a płaszczyzną podstawy to nie miałbym pytań
Jak uzależnić wszystko od H ?
Jak by kąt α był międy krawędzią boczną a płaszczyzną podstawy to nie miałbym pytań

 wskazówka:
wykorzystaj trójkąt utworzony przez wysokość, wysokość ściany bocznej i połowę podstawy.
wskazówka:
wykorzystaj trójkąt utworzony przez wysokość, wysokość ściany bocznej i połowę podstawy.

 potrzebujesz długości podstawy, powiedzmy a.
Teraz liczymy wysokość ściany bocznej
potrzebujesz długości podstawy, powiedzmy a.
Teraz liczymy wysokość ściany bocznej
 chodziło mi o coś takiego.
chodziło mi o coś takiego.
 najpierw z niebieskiego wysokość ściany bocznej potem czerwony i Pitagoras
dlaczego? w niebieskim jest α, a w czerwonym H − twoje wszystkie dane
najpierw z niebieskiego wysokość ściany bocznej potem czerwony i Pitagoras
dlaczego? w niebieskim jest α, a w czerwonym H − twoje wszystkie dane


 W ΔSEC:
W ΔSEC:



 Pozdrawiam!
Pozdrawiam!
 tylko pierwsza opcja a czemu pytasz ?
tylko pierwsza opcja a czemu pytasz ?


 Coś prostego.
Dany jest graniastosłup prawidłowy trójkątny o krawędzi podstawy równej 2√3 i wykości równej
3. Graniastosłup ten przecięto płaszczyzną zawierającą krawędź podstawy i nachyloną do
płaszczyzny podstawy pod kątem 30 stopni. Obliczu pole otrzymanego przekroju.
Coś prostego.
Dany jest graniastosłup prawidłowy trójkątny o krawędzi podstawy równej 2√3 i wykości równej
3. Graniastosłup ten przecięto płaszczyzną zawierającą krawędź podstawy i nachyloną do
płaszczyzny podstawy pod kątem 30 stopni. Obliczu pole otrzymanego przekroju.


 Wewnątrz kąta o mierze 600 znajduje się punkt A odległy od jednego z ramion o 3 a od drugiego
o 6. Oblicz odległość punktu A od wierzchołka kąta.
Wewnątrz kąta o mierze 600 znajduje się punkt A odległy od jednego z ramion o 3 a od drugiego
o 6. Oblicz odległość punktu A od wierzchołka kąta.
 0
0


 For Damian.
For Damian.

 odp. jest dobra
odp. jest dobra
 ja od razu zły trop obrałem
ja od razu zły trop obrałem 

 Jeszcze źle ?
Jeszcze źle ?

 (chyba
(chyba  ).
Po prostu musiałem iść
).
Po prostu musiałem iść  Dziękuję Mila za kontynuację problemu
Dziękuję Mila za kontynuację problemu 
 h=3
h=3