
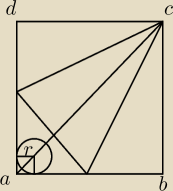
 hmmm?
hmmm?
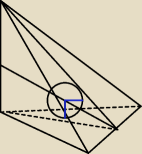
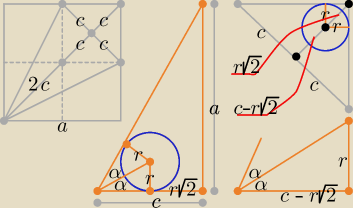 Mało miejsca na rysunki.
4c = a√2 ⇒ c = ...
Mało miejsca na rysunki.
4c = a√2 ⇒ c = ...
| a | 2tgα | r | |||
= tg2α = | ⇒ tgα = ... i tgα = | r = ... | |||
| c | 1 − tg2α | c − r√2 |
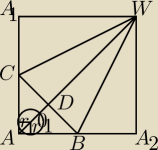 rozwiązałem to tak
rozwiązałem to tak
| 1 | 3 | |||
AW=a√2, A0D= | a√2=AD, DW= | a√2,A0O1=r√2 | ||
| 4 | 4 |
| α |
|
| ||||||||||||||||||||||||||||
O1D=r* ctg | = r * | = r | = | |||||||||||||||||||||||||||
| 2 |
|
|
| 1+cosα |
| DW+A0D | |||||||||||||
r | = r | = r* | = | ||||||||||||
| sin α |
| A0W |
| AW | a√2 | |||
r | =r | =r√2 | ||
| A0W | a |
| 1 | 1 | |||
A0D=A0O1D ⇒ | a√2=r√2+r√2⇒r= | a | ||
| 4 | 8 |
| 1 | ||
Dokończę swoje rozwiązanie: c = | a√2 | |
| 4 |
| a | 2tgα | ||||||||
= tg2α ⇒ | = 2√2, α∊(0o, 90o) | ||||||||
| 1 − tg2α |
| −1 + 3 | 1 | |||
√2tg2α + tgα − √2 = 0, Δ = 9, tgα = | = | |||
| 2√2 | √2 |
| r | 1 | 1 | |||||||||
= | ⇒ r = | a | |||||||||
| √2 | 8 |