bryły
Radek:
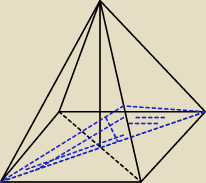
Wysokość ostrosłupa prawidłowego czworokątnego jest 2 razy dłuższa od krawędzi jego podstawy.
Przez przekątną podstawy i środek rozłącznej z nią krawędzi bocznej poprowadzono płaszczyznę.
Czy taki rysunek
29 mar 20:07
Saizou :
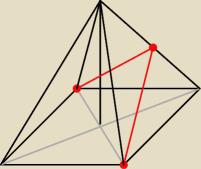
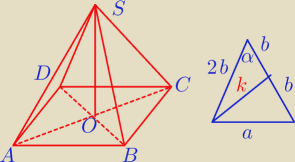
tak lepiej widać xd
29 mar 20:12
Radek:
Dziękuję.
29 mar 20:12
Radek:
Wysokość ostrosłupa prawidłowego czworokątnego jest 2 razy dłuższa od krawędzi jego podstawy.
Przez przekątną podstawy i środek rozłącznej z nią krawędzi bocznej poprowadzono płaszczyznę.
Oblicz pole otrzymanego przekroju, wiedząc, że krawędź podstawy ostrosłupa ma długość a .
| | 3√2a | |
Wyznaczyłem długość krawędzi bocznej |
| |
| | 2 | |
a dalej nie wiem co mam wyznaczać bo nie wiem czy te odcinki to wyokości ?
29 mar 21:18
mietek: musisz to zbadać...
29 mar 21:42
Marcin:
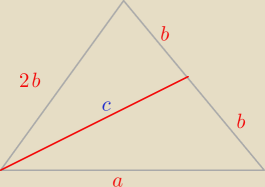
b znasz.
Może to Ci jakoś pomoże

29 mar 21:43
Radek:
| | 3√2a | |
Nie bardzo mam b= |
| i a i co teraz twierdzenie cosinusów ? z tego wyliczę c ? |
| | 4 | |
29 mar 22:02
mietek: cosinus kąta między 2b i b możesz policzyć z cosinusów.
potem to samo twierdzenie dla małego trójkąta i masz c

chyba, że znasz wzór na środkową w trójkącie

29 mar 22:04
Radek:
Znam wzór na środkową
29 mar 22:05
mietek: to możesz od razu podstawić, bo c jest środkową.
29 mar 22:06
mietek: ogólnie to po co ci c

masz policzyć pole przekroju.
przekrój to trójkąt
| | 1 | |
wzór na pole trójkąta to... P= |
| ah |
| | 2 | |
podstawę masz.
potrzebujesz wysokości trójkąta...
robisz to z innego trójkąta.
29 mar 22:09
Marcin:
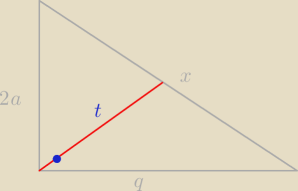
Możesz też tak.
Znasz q, bo to przekątna kwadratu czyli ma a
√2
29 mar 22:11
Radek:
OK, dziękuję zapomniałem o wzorze na środkową.
29 mar 22:12
Marcin: środkowa opuszczona na przeciwprostokątną dzieli trójkąt na dwa trójkąty równoramienne
W sumie nawet o tym nie wiedziałem.

29 mar 22:16
29 mar 22:21
Marcin: Napisałem Ci przecież, że to połowa krawędzi bocznej twojego ostrosłupa.
| | 3√2 | |
czyli według tego co Ty obliczyłeś (nie sprawdzałem), to t ma mieć |
| . Co to u Ciebie |
| | 4 | |
ramie tego trójkąta?
29 mar 22:26
Marcin: C* to u Ciebie ramie?
29 mar 22:26
Radek:
Liczę z twierdzenia cosiunusów
a
2=(2a)
2+(2a)
2−2*2a*2a*cosα
| | 3√2a | | 3√2a | | 7 | |
c2=(UP3√2a}{2})2+ |
| )2−2*(UP3√2a}{2})+ |
| )* |
| |
| | 4 | | 4 | | 8 | |
29 mar 22:31
Marcin: Odpowiedź masz ok, ale gdzie znalazłeś taki trójkąt, co?

29 mar 22:39
Radek:
w arkuszu
29 mar 22:42
Radek:
ale coś mi nie pasuję cos chyba tak liczyć trzeba
| | 3√2a | |
x−długość krawędzi bocznej |
| |
| | 2 | |
| | 3√2a | | 3√2a | | 3√2a | | 3√2a | |
a2=( |
| )2+( |
| )2−2* |
| * |
| *cosα ? |
| | 2 | | 2 | | 2 | | 2 | |
29 mar 22:53
Radek: ?
29 mar 23:02
Marcin: No tak już szybciej, ale w tym zadaniu nie ma co kombinować

Jak miałbyś już cosx, to maszliczysz krawędź przekroju, a jak masz już krawędź, to jesteś w
domu

29 mar 23:05
Radek:
To teraz wyszło mi inaczej
29 mar 23:13
Marcin: | | 4 | |
A jaki Ci wyszedł cos? |
| ? |
| | 9 | |
29 mar 23:18
bezendu:
| 8 | |
| raczej z tego co ja policzyłem |
| 9 | |
29 mar 23:18
Marcin: | | 18a2 | | 18a2 | | 18a2 | |
a2= |
| + |
| −2* |
| *cosα |
| | 4 | | 4 | | 4 | |
a
2=9a
2−18a
2*cosα
−8a
2=−18a
2*cosα
Chyba że się gdzieś walnąłem

29 mar 23:26
Marcin: ok, już wiem gdzie

powinno być −9cosα

29 mar 23:27
Domel:
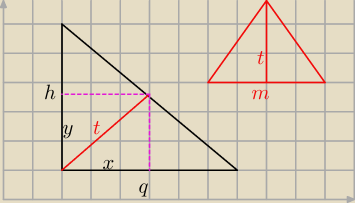
Odnośnie rysunku
marcina z 22:11 − rysunek dobry ale q to nie przekątna podstawy tylko
połowa przekątnej
t − to wysokość trójkąta (patrz czerwony trójkąt
Saizou z 20:12)
h = 2a
y = a
m =
√2a − przekątna podstawy
| | 1 | | 9 | |
t2 = x2 + y2 = |
| a2 + a2 = |
| a2 |
| | 8 | | 8 | |
| | 3 | | 3 | | 3√2 | |
t = |
| a = |
| a = |
| a |
| | √8 | | 2√2 | | 4 | |
no i mamy czerwony trójkąt
| | 3√2 | | 3*2 | |
P = 0,5*m*t = 0,5 * √2a * |
| a = |
| a2 |
| | 4 | | 4 | |
30 mar 13:01
Domel:
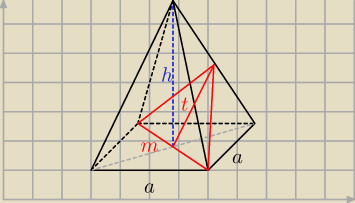
30 mar 13:11
Radek:
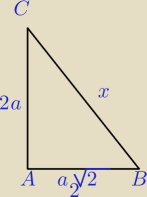
x−krawędź boczna
| | 3√2a | | 3√2a | | 3√2 | | 3√2 | |
cosα=( |
| )2+( |
| )2−2* |
| * |
| *cosα |
| | 2 | | 2 | | 2 | | 2 | |
| | 3√2a | | 3√2a | | 3√2a | | 3√2a | | 8 | |
c2=( |
| )2+( |
| )2−2* |
| * |
| * |
| |
| | 2 | | 4 | | 2 | | 4 | | 9 | |
Pole wychodzi inne niż w odp gdzie błąd ?
30 mar 15:24
Radek: ?
30 mar 15:36
Radek: ?
30 mar 15:56
Mila: Tyle komentarzy..
Napisz jaka treść do rozwiązania.
30 mar 16:12
Radek: Wysokość ostrosłupa prawidłowego czworokątnego jest 2 razy dłuższa od krawędzi jego podstawy.
Przez przekątną podstawy i środek rozłącznej z nią krawędzi bocznej poprowadzono płaszczyznę.
Oblicz pole otrzymanego przekroju, wiedząc, że krawędź podstawy ostrosłupa ma długość a .
i chodzi o moje rozwiązanie 15:24
30 mar 16:17
Mila:
Krawędź dobrze, ale zapomniałeś o a.
W ΔABC:
Wysokość przekroju liczysz :
| | a√2 | | 3a√2 | |
h2=( |
| )2+( |
| )2−2*.... to już dokonczysz na pewno |
| | 2 | | 4 | |
30 mar 16:36
Radek:
| | 8 | |
nie może wyjść taki cosinus przecież rozpisałem i wychodzi |
| ? |
| | 9 | |
30 mar 16:40
Mila:
3 linijka z 15:24 w jakim to Δ i dlaczego po obu stronach jest cosα?
30 mar 16:44
Radek:
tam powinno być a2=i dalej to samo
30 mar 16:56
Radek:
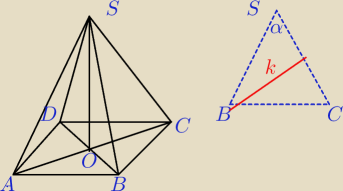
30 mar 16:58
Mila:
Niejednoznaczne są oznaczenia, w każdym wątku co innego.
Po co liczysz bok przekroju zamiast wysokość.
30 mar 17:05
Radek:
Chcę policzyć bok aby wyznaczyć wysokość przekroju.
30 mar 17:07
Marcin: To takie trochę robienie pod górkę, ale też się da

30 mar 17:07
Radek: wiem,że pod górke ale chce tak zrobić
30 mar 17:11
Mila:
Przecież możesz obliczyć cosinus kąta SCO ( tak Ci poradziłam) i potem od razu liczysz wysokość
przekroju.
Twoim sposobem więcej pracy, ale też wychodzi.
| | 3√2 | |
hprzekroju= |
| z tw. Pitagorasa. |
| | 4 | |
15:24 popraw ostatnią linikę.
30 mar 17:22
bezendu:
| | 3√2a | | 3√2a | | 3√2a | | 3√2a | |
a2=( |
| )2+( |
| )2−2* |
| * |
| *cosα |
| | 2 | | 4 | | 2 | | 4 | |
a
2=9a
2−9cosα
| | 3√2a | | 3√2a | | 3√2a | | 3√2a | | 8 | |
k2=( |
| )2+( |
| )2−2* |
| * |
| * |
| |
| | 4 | | 2 | | 4 | | 2 | | 9 | |
| | √26 | | a√2 | |
hprzekroju=( |
| )2−( |
| )2 |
| | 4 | | 2 | |
I wyszło poprawnie

30 mar 17:34
bezendu:
Mila zapomniałaś o a w wysokości przekroju
30 mar 17:51
Mila:
Dobrze. Bezendu rozwiązałeś zadanie z wycieraczką?
30 mar 17:55
Mila:
Wiem, że zapomniałam, czekałam, aż Radek to zauważy.
30 mar 17:56
bezendu:
Nie jeszcze, po 20 za nie się zabiorę teraz robię bryły bo muszę poprawić, żeby ładna ocena
była na świadectwie.
30 mar 17:56
Radek: Dziękuję, już wiem gdzie robią błąd.
30 mar 17:57
Marcin: A jaka to jest ładna?

30 mar 17:57
Mila:
Zaraz dam Ci bryłkę, załóż nowy wątek, właśnie przygotowałam dla Ciebie 2 zadanka ze
stereometrii.
30 mar 17:58
bezendu:
A to tajemnica.

Ale możesz się domyślać.
30 mar 17:58
Piotr 10: Wiadomo, że piąteczka

30 mar 17:59
bezendu:
A może number 2

30 mar 17:59
Piotr 10: Hehe

30 mar 18:00
Marcin: ehee dwaa

30 mar 18:01
bezendu: Powiem Wam dopiero pod koniec kwietnia

30 mar 18:03
Radek:
bezendu zgubiłeś w 3 linicje a
2 
30 mar 18:49
Radek:
Już mam nawet dwoma sposobami.
30 mar 20:39
Marcin: brawo

fajnie że jesteś konsekwentny i jak zaczynasz jednym sposobem, to chcesz nim kończyć

No czekam bezendu na tą ocenę

Jeszcze nam z celującym wyskoczysz

30 mar 20:42
Piotr 10: Ja to mam dostateczny xD
30 mar 20:42
bezendu:

30 mar 20:43
Mila:
Brawo,Radek, myślałam, że zniechęciłeś się.
30 mar 20:47
Marcin: Ja liczę na 5, ale nie wiem co z tego wyjdzie

30 mar 20:47
Piotr 10: To ładnie

30 mar 20:48
Marcin: Ale ja nie mam rozszerzenia u siebie w szkole

30 mar 20:49
Radek:
Pani Milu ja nigdy się nie poddaję ! Teraz jeszcze zostały te nierówności z
prawdopdobieństwa typu wykaż, pomoże Pani ?
30 mar 20:51
Mila:
Zostaw je na razie, ćwicz geometrię analityczną. Za zadania z geometri jest więcej punktów do
stracenia.
Rozwiązuj zadania z treścią z ciągów.
30 mar 21:01
Radek: Dobrze to zaraz będę szukał tej geometrii analitycznej.
30 mar 21:10
Domel: bezendu co to za trójkąt z prawej strony na twoim poście z 17:34
Wydaje mi się, że moje szkice z 13:01 i 13:11 były poprawne. No i wynik pola masz 2 razy
mniejszy.
Może ktoś sprawdzi, które działania są poprawne


30 mar 23:49
bezendu:
to trójkąt BSC , jutro poprawię bo chyba wiem gdzie błąd.
30 mar 23:52
Marcin: To jest ściana boczna ostrosłupa

30 mar 23:53
bezendu: Podałem źle na końcu
| | 3√2a | | 3a2 | |
Pole przekroju P=0,5* |
| *a√2= |
| zadowolony  ? A kto mi zabroni tak zrobić |
| | 4 | | 4 | |
zadanie ?
30 mar 23:55
Domel: Oki − zapomniałem w moich obliczeniach w ostatniej linijce o pomnożeniu przez 0,5 dlatego
miałem inny wynik i szukałem gdzie się wkradł feler

31 mar 00:40
bezendu:
To miód malina

Ale dzięki za poprawkę

31 mar 00:41
 Wysokość ostrosłupa prawidłowego czworokątnego jest 2 razy dłuższa od krawędzi jego podstawy.
Przez przekątną podstawy i środek rozłącznej z nią krawędzi bocznej poprowadzono płaszczyznę.
Czy taki rysunek
Wysokość ostrosłupa prawidłowego czworokątnego jest 2 razy dłuższa od krawędzi jego podstawy.
Przez przekątną podstawy i środek rozłącznej z nią krawędzi bocznej poprowadzono płaszczyznę.
Czy taki rysunek
 tak lepiej widać xd
tak lepiej widać xd
 b znasz.
Może to Ci jakoś pomoże
b znasz.
Może to Ci jakoś pomoże 
 chyba, że znasz wzór na środkową w trójkącie
chyba, że znasz wzór na środkową w trójkącie 
 masz policzyć pole przekroju.
przekrój to trójkąt
masz policzyć pole przekroju.
przekrój to trójkąt
 Możesz też tak.
Znasz q, bo to przekątna kwadratu czyli ma a√2
Możesz też tak.
Znasz q, bo to przekątna kwadratu czyli ma a√2


 Jak miałbyś już cosx, to maszliczysz krawędź przekroju, a jak masz już krawędź, to jesteś w
domu
Jak miałbyś już cosx, to maszliczysz krawędź przekroju, a jak masz już krawędź, to jesteś w
domu 

 powinno być −9cosα
powinno być −9cosα

 Odnośnie rysunku marcina z 22:11 − rysunek dobry ale q to nie przekątna podstawy tylko
połowa przekątnej
t − to wysokość trójkąta (patrz czerwony trójkąt Saizou z 20:12)
h = 2a
Odnośnie rysunku marcina z 22:11 − rysunek dobry ale q to nie przekątna podstawy tylko
połowa przekątnej
t − to wysokość trójkąta (patrz czerwony trójkąt Saizou z 20:12)
h = 2a

 x−krawędź boczna
x−krawędź boczna





 Ale możesz się domyślać.
Ale możesz się domyślać.






 fajnie że jesteś konsekwentny i jak zaczynasz jednym sposobem, to chcesz nim kończyć
fajnie że jesteś konsekwentny i jak zaczynasz jednym sposobem, to chcesz nim kończyć
 No czekam bezendu na tą ocenę
No czekam bezendu na tą ocenę  Jeszcze nam z celującym wyskoczysz
Jeszcze nam z celującym wyskoczysz 







 ? A kto mi zabroni tak zrobić
? A kto mi zabroni tak zrobić
 Ale dzięki za poprawkę
Ale dzięki za poprawkę 