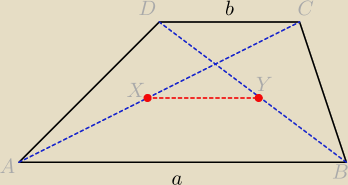
Marcin: Dany jest trapez o podstawach a i b, gdzie a>b. Wyznacz długość odcinka łączącego środki przekątnych. Jakieś podpowiedzi?

Piotr 10: ΔACB

	a
Przedłuż odcinek czerwony to boku CB, wtedt długość będzie równa
	2

ΔDCB podobnie

Saizou :

	a−b
lXYl=		jak dobrze pamiętam
	2

Marcin:

	a
Dlaczego ten odcinek to będzie		?
	2

5-latek: Saizou dobrze pamietasz

Marcin: Saizou dobrze pamiętasz, ale mi chodzi bardziej o sposób rozwiązania niż o odpowiedź

[brązowy]marcos: Odcinke łączący te środki ramion to połowa sumy podstawy

Piotr 10: Odcinek łączacy środki dwóch boków jest rownolegly do trzeciego boku i równy polowie jego dlugosci ( wynika to z podobieństwa )

Marcin: Dzięki. Może jakoś to przekompiluję

Saizou : można też z wektorów

Trivial: Wektorowo idzie szybko → 3 linijki bez żadnych magicznych własności trójkątów.

Saizou :

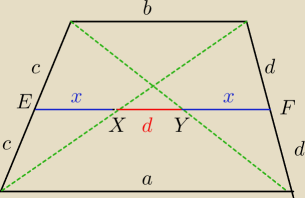
Janek191: Z tw. Talesa mamy

	1
x =		b ⇒ 2 x = b
	2

więc

	a + b		a + b		2 b		a − b
d = I EF I − 2 x =		− b =		−		=
	2		2		2		2

[brązowy]marcos: fajnie rozrysowałeś, teraz wszystko jak na tacy

Marcin: oo Janek. Wielkie dzięki. Teraz to widzę Nie wiedziałem, że |EX|=|YF|

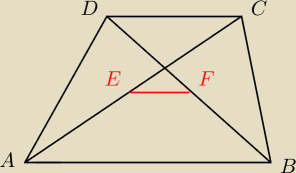
Saizou : zapisze bez strzałek nad wektorami:

	1		1
EF=		CA+AB+		BD
	2		2

	1		1
EF=		AC+CD+		DB
	2		2

=========================+ 2EF=AB−CD

	AB−CD		a−b
EF=		⇒EF=
	2		2

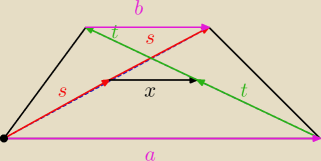
Trivial: Rozwiązanie wektorowe. Przyjmując odniesienie wszystkich wektorów w punkcie 0 mamy: s + x = a + t → x = a + t−s a + 2t + b = 2s → t−s = −¹₂(a+b)

	a−b
Zatem x = a − 12(a+b) =		(wektorowo). Wracając do świata odległości mamy:
	2

	a−b
x =		.
	2

Saizou : fajnie określenia "świat odległości"

Marcin: Wielkie dzięki Panowie za wektory

Trivial: Saizou, dobre określenia to podstawa.

Saizou : a podstawa to nie a lub b

Trivial: Saizou, idziesz na matematykę?

Saizou : na razie to siedzę, a sam już nie wiem gdzie iść na studia

5-latek: Dla mnie podstawa to jak dobrze napisac podanie o podwyzke do szefa w zwiazku z tym ze ma zdrozec margaryna w Biedronce )