pole Jakubek: Cięciwy AB i CD przecinają się w punkcie E, |AEC| = 45. Wiedząc, że |AE| = 4, |CE| = 2, |ED| = 3, oblicz: a) pole trójkąta AEC b) pole trójkąta BED. Najkrótszy bok trójkąta ABC ma 10 cm długości, a miary jego kątów są w stosunku 3 : 2 : 1. Oblicz: a) pole trójkąta ABC b) pole koła wpisanego w trójkąt ABC Pomoże ktoś?

Jakubek: W 2 zadaniu wiadomo, że trójkąt bedzie miał kąty 30,60,90

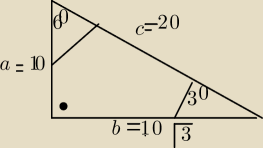
5-latek: Z trojkata o katach 30 60 90 wynikaja te jego wymiary

	10√3*10
Pole=		= policz
	2

	a+b−c
r=		−− taki jest wzor na promien okregu (kola ) wpisanego w trojakt prostokatny
	2

P_k=pir²

Jakubek: r=10+10√3−20/2 r=−10+10√3/2 r=−5+5√3 P=pir² po zastosowanie wzoru skróconego mnożenia wyjdzie 100+50√3 ?