funkcje trudne Krzyś: Dane są funkcje f i g określone wzorem f(x) =1/2 x + 2 i g(x) = − x −1 a) Sporządz wykres tych funkcji w jednym układzie współrzednych, b) Dla jakiego argumentu obie funkcje mają tę samą wartość? wyznacz te wartość c) Dla jakich argumentów funkcja f przyjmuje wartości większe od wartości funkcji f? d) dla jakich argumentów obie funkcje przyjmują wartości dodatnie?

Krzyś: pomoże ktoś?

[brązowy]marcos: a) podaj jakieś wartości do x, dostaniesz y, narysuj układ współrzędnych i połącz,

[brązowy]marcos: mam namyśli punkty jednej funkcji i oddzielnie drugiej...

Krzyś: pomożesz mi do 1 podpunktu?

[brązowy]marcos: cóż, to jest najprostsza czynność, jaką można wykonać

[brązowy]marcos: pisze z komorki, nie narysuje ci wykresu

Krzyś: nie chcę wykresu tylko nie wiem co i gdzie mam podstawić

[brązowy]marcos: f(x) =1/2 x + 2 i g(x) = − x −1 podstawiasz dowolnej wartości pod x danej funkcji, otrzymujesz współrzędne punktów, później je łączysz? x | 1 | 2| f(x) =1/2 x |1/2| 1| podobnie z drugą funkcją

Janek191:

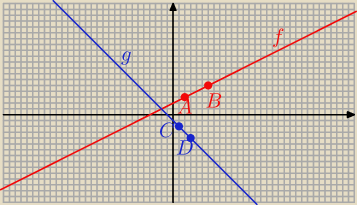
	1
f(x) =		x + 2 g(x) = − x − 1
	2

	1
a) Dla x = 2 jest f(2) =		*2 + 2 = 3 A = ( 2; 3)
	2

	1
Dla x = 6 jest f(6) =		*6 + 2 = 5 B = ( 6; 5)
	2

Prosta AB to wykres funkcji f. Dla x = 1 jest g(1) = − 1 − 1 = − 2 C = ( 1; − 2) Dla x = 3 jest g(3) = − 3 − 1 = − 4 D = ( 3; − 4) Prosta CD to wykres funkcji g. Rysunek. b) f(x) = g(x)

1
	x + 2 = − x − 1 / * 2 Rozwiąż to równanie
2

c) Popraw treść pytania c.

Jakub pała: αβγδπΔΩ∞≤≥∊⊂