pole czworokąta beata: W tapezie połączono środki boków otrzymując czworokąta KLAN. a)udowodnij, że czworokąt KLMN jest rownoleglobokiem b)oblicz pole czworokąta KLMN wiedząc że przekątne trapezoidu przecinają się pod kątem 30° a jego pole jest równe 24cm².

PW: Co to za jeden ten KLAN?

beata: Przepraszam miało być KLMN

Janek191: Czy mamy trapez , czy trapezoid ?

beata: Trapezoid

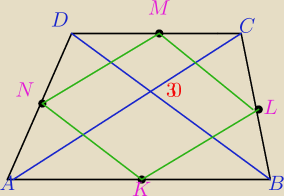
5-latek: Narysowalem CI to dla trapezu A teraz zobacz co to jet trapezoid i napisz czy ma byc trapez czy trapezoid

5-latek: No to skoro wiesz co to trapeziod to jaki problem narysowac to ?

beata: Przepraszam za pomylki. spieszyłam się przepisując

beata: Z narysowaniem nie ma problemu gorzej z udowodnieniem i dobrymi obliczeniami

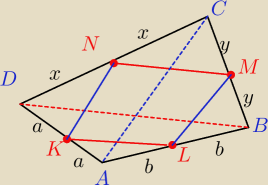
Janek191: W dowodzie korzystamy kilkakrotnie z Tw. Talesa.

Janek191:

	x		y
Np.		=		= 1, więc odcinek MN jest równoległy do odcinka BD.
	x		y

a		b
	=		= 1 , więc odcinek KL jest równoległy do odcinka BD
a		b

zatem odcinki MN i KL są równoległe. Podobnie dowodzi się równoległość odcinków KN i LM.

Janek191: b) Jeżeli pole trapezoidu jest równe 24 cm², to pole równoległoboku KLMN jest równe

1
	*24 cm2 = 12 cm2.
2

=====================

beata: Skąd wiemy że pole tego rownolegloboku to jest połowa pola tego trapezoidu?

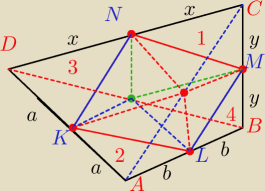
Janek191: P − pole trapezoidu ABCD P₁ − pole Δ_MNC P₂ − pole Δ_KLA P₃ − pole Δ_KND P₄ − pole Δ_LMB Mamy

	1
P1 =		PΔBCD
	4

	1
P2 =		PΔABD
	4

więc

	1		1
P1 + P2 =		*( PΔBCD + PΔABD) =		P
	4		4

oraz

	1
P3 =		PΔACD
	4

	1
P4 =		PΔABC
	4

więc

	1		1
P3 + P4 =		*( PΔACD + PΔABC) =		P
	4		4

dlatego

	1		1		1
P1 + P2 + P3 + P4 =		P +		P =		P
	4		4		2

czyli pole równoległoboku KLMN jest równe

	1		1
Pr = P − (P1 + P2 + P3 + P4) = P −		P =		P
	2		2

===============================================