pole czworokąta beata: W romb ABCD o boku długości 5 wpisano prostokąt PQRS w taki sposób, że boki prostokąta są równoległe do przekątnych rombu. Oblicz, o ile procent pole prostokąta jest mniejsze od pola rombu, wiedząc dodatkowo, że krótsza przekątna rombu ma długość 6 a obwód prostokąta jest równy 14,4

beata: Proszę o pomoc

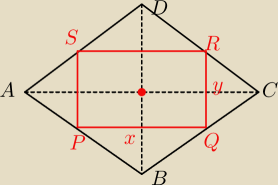
Janek191: I BD I = 6 ⇒ b = 0,5 I BD I = 3 a = I AB I = I BC I = I CD I = I AD I = 5 L_p = 14,4 0,5 I AC I = c Z tw. Pitagorasa mamy c² + b² = a² c² = a² − b² = 5² − 3² = 16 c = √16 = 4 Pole rombu P_r = 0,5*I AC I * I BD I = 0,5*8*6 = 24 ============================= L_p = 2 x + 2y = 14,4 ⇒ x + y = 7,2 ⇒ y = 7,2 − x oraz

x		3 − 0,5 y
	=
I AC I		3

x		3 − 0,5*(7,2 − x)
	=
8		3

x		3 − 3,6 + 0,5 x
	=
8		3

3 *x = 8*( 0,5 x − 0,6) 3 x = 4 x − 4,8 x = 4,8 ===== y = 7,2 − 4,8 = 2,4 ============= Pole prostokąta P_p = x*y = 4,8* 2,4 = 11,52 zatem

24 − 11,52		12,48
	=		=0,52 = 52 %
24		24

Odp. Pole prostokąta jest mniejsze o 52 % od pola rombu. ===========================================