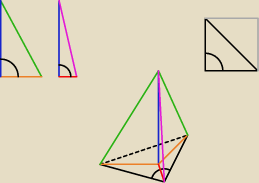
 Podstawą ostrosłupa jest trójkąt równoramienny prostokątny o przeciwprostokątnej długości
2√2. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 60 stopni. Oblicz
pole powierzchni bocznej tego ostrosłupa.
Wydaje mi się, że tylko w ostrosłupach prawidłowych krawędzie boczne mogą być nachylone pod
kątem o tej samej wartości. Pewnie się mylę. Jak to rozwiązać?
Podstawą ostrosłupa jest trójkąt równoramienny prostokątny o przeciwprostokątnej długości
2√2. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 60 stopni. Oblicz
pole powierzchni bocznej tego ostrosłupa.
Wydaje mi się, że tylko w ostrosłupach prawidłowych krawędzie boczne mogą być nachylone pod
kątem o tej samej wartości. Pewnie się mylę. Jak to rozwiązać?
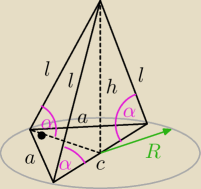 α = 60o
c = 2√2
α = 60o
c = 2√2
| c√2 | ||
a = | = 2 | |
| 2 |
| c | ||
R = | = √2 | |
| 2 |
| h | |
= tg60o = √3 | |
| R |
| R | 1 | ||
= cos60o = | |||
| l | 2 |
| (c*h) + (a*l) + (a*l) | ||
Pb = | = | |
| 2 |