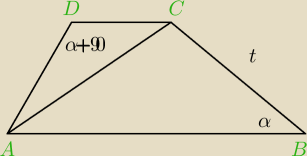
plani jerey: W pewnym trapezie kąty przy dwóch przeciwległych wierzchołkach mają miary α oraz 90⁰ + α . Jedno z ramion tego trapezu ma długość t . Wyznacz różnicę długości podstaw tego trapezu. zacząłem z twierdzenia cosinusów, uzywając przekatnej AC; AC²=DC²+AD²−2AD*DC*cos(90⁰+α) AC²=DC²+AD²−2AD*DC*(−sinα) AC²=DC²+AD²+2AD*DC*sinα AC²=t²*AB²−2t*AB*cosα lecz nie wiem czy do czegokolwiek to prowadzi. Prosiłbym o jakies wskazówki bo nie mam koncepcji na to zadanie.

Tadeusz: ... opuść wysokość trapezu z punktu D Przetnie ona AB w punkcie E Jaki jest kąt ADE

Tadeusz: opuść wysokość z punktu C .. przetnie AB w puncie F Policz |FB| policz h policz |AE| |AE+|FB| to szukana różnica długości podstaw

jerey: ok, licze

jerey: wyszło AB − DC = tsinα+tcosα=t(sinα+cosα)

Tadeusz: ... nie chce mi się liczyć − ....to już tylko rachunki −

Eta: a>b , |AD|=t W trójkącie prostokątnym DCE i ABE :

	k
		=sinα ⇒ k=b*sinα
	b

	t+k
		=sinα ⇒t+k=a*sinα
	a

− −−−−−−−

	t
t=(a−b)*sinα ⇒ a−b=
	sinα

	t		t
lub jeżeli |BC|=t to podobnie ...... otrzymasz a−b=		=
	sin(90−α)		cosα

jerey: dzieki, nie wpadłbym ,ze trzeba rozbijac trapez do trójkąta i to prostokątnego.