zadankowo Saizou : witam Was ma ktoś zadanka maturalne, nie z zadania.info czyli czas na seria powtórek do matury

zawodus: Jak trudne?

Saizou : niby poziom rozszerzony, ale wiem że masz zawodusie problemy z rozpoznaniem poziomu, wiec może na początek poziom średni

zawodus: Jaka tematyka? Ostatnio coraz lepiej mi idzie

Saizou : tematyka to co do matury 2014 powinienem umieć xd no to gratki

zawodus: Ok to zadanie pierwsze. Teoria liczb: 1. Wyznacz wyznacz wszystkie liczby całkowite a dla których liczba postaci

	a2+2a+2
		jest liczbą całkowitą
	a+1

Na początek bardzo proste

zawodus: Tylko dział nie do końca taki (bardziej to wyrażenia arytmetyczne )

Saizou : zał a≠−1

(a+1)2+1		1
	=a+1+		, zatem a+1=1⇒a=0, bo dla a≠−1
a+1		a+1

Saizou : co ja napisałem miało być a+1=1 lub a+1=−1 a=0 lub a=−2

zawodus: chyba za łatwe było

Piotr: a −2 ?

Piotr: ok, cofam

Saizou : chwila dekoncentracji i już błąd się wkradł

zawodus: Dobra zadanie 2 2. Dany jest trójkąt ABC, gdzie A=(2,−9), B=(8,3). Na paraboli y=x²+6x+5 znajdź punkt C tak, aby pole trójkąta miało wartość najmniejszą.

zawodus: Od razu zadanie 3. 3. Dany jest trapez o podstawach długości 14 i 8. Suma kątów w tym trapezie przy krótszej podstawie jest równa 270^o. Uzasadnij, że odcinek łączący środki podstaw trapezu ma długość 3.

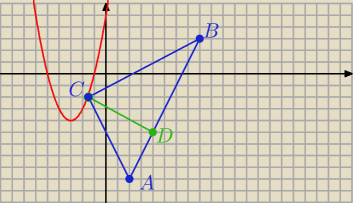
Saizou : C=(x:x²+6x+5) A=(2:−9) B=(8:3)

	1
PABC=		lABl*lCDl
	2

najmniejsza wartość tego pola jest gdy CD jest najmniejsze zatem CD to odległość punktu CD od prostej AB prosta AB ma wzór y=2x−13⇒2x−y−13=0

	l2x−12(x2+6x+5)−13l		l−12x2−70x−73l
CD=		=		, a to coś ma najmniejszą
	√4+169		√173

	70   √173		70		35
wartość dla xw=		=		=−
	12   −2*   √173		−24		12

	35		35		575
y=(−		)2+6*(−		)+5=−
	12		12		144

ale coś mi te wyniki nie pasują xd

zawodus: Przekombinowałeś szukaj błędu

Saizou : α+β=270 γ+δ=90

	14−8
odcinek łączący środek podstaw trapezu to R−r, zatem		=3
	2

Saizou : ogólnie to bym wrzucił do wzoru na pole trójkąta z wierzchołków ale nie chciało mi się szukać xd

zawodus: Zadanie 3 jest ok. Drugie do czeka na poprawkę cały czas Chyba, że pokażesz błąd to daruje ci je

Saizou : tam nie powinno być −12 a −1 , zatem wyjdzie x_w=−2 y_w=−3

zawodus: Dobra jest ok chwila na wymyślenie zadania

Piotr 10: Saizou chcesz ode mnie zadanko z ciągami ?

Saizou : a zarzuć może się czegoś nauczę

Piotr 10: Ze skończonego ciągu kolejnych liczb naturalnych nieparzystych 1,3,5,...., 2n−1 wybieramy kilka kolejnych liczb końcowych, których suma wynosi 120. Róźnica kwadratów największej i najmniejszej z wybranych liczb jest równa 360. Znajdź wybrane liczby. Będę później jak cos

zawodus: zadanie 4 (coś szybkiego bo muszę na chwilę lecieć) 4. Basen opróżnia się przez 6 godziny. Pierwszy kran napełnia basen w ciągu 2 godzin, a drugi w ciągu 3 godzin. Jednocześnie odkręcamy oba krany i zaczynamy spuszczać wodę. Oblicz w jakim czasie napełnimy basen?

Saizou : m<n m−najmniejsza z wybranych liczb n− największa z wybranych liczb S_"n−m"=120

2+(n−1)		2+(m−1)
	n−		m=120
2		2

2n+n²−n−2m−m²+m=240 n−m+n²−m²=240 dodatkowo wiemy że n²−m²=360 n−m+360=240 n−m=−120 i coś mi tu nie pasuje bo skoro n>m to n−m>0

pigor: ..., a nie "zjadłeś " w treści zadania słowa ... a drugi opróżnia

zawodus: Jest tak, że mamy dwa krany, które napełniają i "korek" do spuszczania wody

pigor: ...o , przepraszam, już się nie wcinam, chyba wszystko w porządku

Saizou : t=1,5 h?

Piotr: Saizou suma kilku jest rowna 120 a nie najmniejszej i najwiekszej.

pigor: ..., zgadza się

zawodus: zadanie 5 5. Wyznaczyć dziedzinę i zbiór wartości funkcji √2+√x−x. mam nadzieję ża zapis uda się odczytać (pod pierwiastkiem jest 2+√x−x)

Saizou : suma kliku: S_n=a₁+a₂+a₃.........................+a_n S_m=a₁+a₂+a₃+......+a_m(+......+a_n) skoro założyłem że n>m to −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− odejmując stronami S_n−S_m=a_m+....+a_n wiec nie widzę w tym błędu

zawodus: zadanie 4 − tak czas to 1,5h.

Piotr: aha ja wzialem kalkulator i w chwile znalazlem liczby tak jak chcieli

zawodus: Aktualnym problemem jest zadanie nr 5

Saizou : chciałem zrobić algebraicznie

Piotr: napisali znajdz to znalazlem

Saizou : 2+√x−x≥0 √x≥x−2 x≥0 i x−2≥0→x≥2 a dla każdej liczby z <0:2) nierówność zachodzi x≥x²−4x+4 x²−5x+4≤0 (x−4)(x−1)≤0 x∊<1:4> zatem D: x∊<0:4>

Saizou : niby tak, ale jeśli jest bardziej skomplikowane zadanie to może być więcej rozwiązań, których się nie zauważy

Piotr: no pewnie

Robaczek: Nawet nie wiedziałem, że tak można. Nikt mi tego nie pokazywał jak to zrobiłeś: √x≥x−2 x≥0 i x−2≥0→x≥2 Dzięki!

zawodus: dziedzina ok teraz zbiór wartości.

zawodus: Robaczek, tam jest akurat błąd

Robaczek: Wyjaśnisz zanim zapamiętam?

zawodus: Dobra, żartowałem nie ma błędu tylko zapis trochę nieczytelny Wolno podnosić do kwadratu, kiedy obie strony są nieujemne czyli kiedy x≥2

Saizou : chodzi o to żeby móc podnieść do kwadratu to musimy mieć dwie strony dodatnie a dla jakich x−ów x−2 jest dodatnie xd

Saizou : racja, nieujemne

zawodus: zadanie 6 6. Prosta y =13−2x zawiera bok AB trójkąta ABC, prosta y=x−5 zawiera bok BC, a prosta y=3x−7 zawiera dwusieczną kąta ACB. Znajdź wierzchołki tego trójkąta i oblicz jego pole.

Saizou : nie chce mi się już dzisiaj wiec to ostatnie zadanko

zawodus: A byłeś taki zapalony

pigor: ..., zapomnieliście o wartości funkcji z zadania 5

zawodus: Ja pamiętam i czekam

Saizou : byłem ale to o 19 :00

muflon: Czy wierzchołki to będą: A(−4,21) B(6,1) C(1,−4) Pole=74 j²

muflon: a zbiór wartości funcji z 5, to f(x)∊<0,√7/2>

pigor: ..., no to ja postawię na przedział.. <0.³₂>

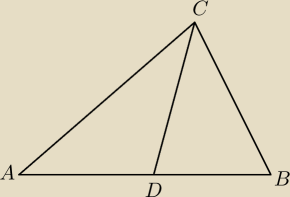
Saizou : A=(x;−2x+13) B=(6;1) C=(1;−4) D=(4;5) z tw. o dwusiecznej kąta w trójkącie

AD		BD
	=
AC		BC

√(4−x)2+(5+2x−13)2		√20
	=
√(1−x)2+(−4+2x−13)2		√50

(4−x)2+(2x−8)2		2
	=
(1−x)2+(2x−17)2		5

16−8x+x2+4x2−32x+64		2
	=
1−2x+x2+4x2−68x+289		5

5x2−40x+80		2
	=
5x2−70x+290		5

25x²−200x+400=10x²−140x+580 15x²−60x−180=0 x²−4x−12=0 (x−6)(x+2)=0 x=−2 x=6 (sprzeczność) A=(−2:17) P=60