 α+β+γ=900⇒β+γ=900−α
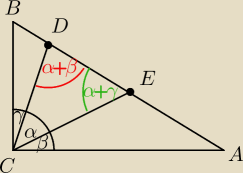
Trójkąt ADC jest równoramienny, bo IACI=IADI. W trójkącie tym kąty przy podstawie są takie
same, czyli ∡D=α+β.
Trójkąt BCE też jest równoramienny, czyli ∡E=α+γ.
Suma miar kątów w trójkącie CED jest równa 1800, czyli:
α+α+β+α+γ=1800
3α+β+γ=1800, ale wiemy, że β+γ=900−α czyli
3α+900−α=1800
2α=900
α=450
α+β+γ=900⇒β+γ=900−α
Trójkąt ADC jest równoramienny, bo IACI=IADI. W trójkącie tym kąty przy podstawie są takie
same, czyli ∡D=α+β.
Trójkąt BCE też jest równoramienny, czyli ∡E=α+γ.
Suma miar kątów w trójkącie CED jest równa 1800, czyli:
α+α+β+α+γ=1800
3α+β+γ=1800, ale wiemy, że β+γ=900−α czyli
3α+900−α=1800
2α=900
α=450
 Mamy
α + β = 90o
Mamy
α + β = 90o
| 180o − α | ||
I ∡ ADC I = | ||
| 2 |
| 180o − β | ||
I ∡ BEC I = | ||
| 2 |
| 180o | 180o | |||
δ + | + | = 180o | ||
| 2 | 2 |
| 360o − ( α + β) | ||
δ + | = 180o | |
| 2 |
| 360o − 90o | ||
δ + | = 180o | |
| 2 |
| 180o − α | 180o − β | |||
δ + | + | = 180o | ||
| 2 | 2 |

