Stereometria, ostrosłup czworokątny prawidłowy jup: w ostrosłupie czworokątnym prawidłowym stosunek wysokości ściany bocznej, poprowadzonej z wierzchołka ostrosłupa, do wysokości ostrosłupa wynosi 5:3. Oblicz kosinus kąta pomiędzy sąsiednimi ścianami bocznymi.

GIBON: Wynik = cos=0,59

jup: jakieś obliczenia?

dero2005:

hs		5
	=
H		3

	3
H =		hs
	5

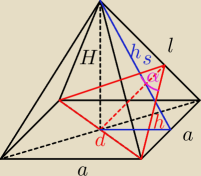
H² + (^a₂)² = h_s² (³₅h_s)² + (^a₂)² = h_s²

	5
hs =		a
	8

h_s² + (^a₂)² = l²

	√41
l =		a
	8

a*h_s = h*l

	a*hs		5
h =		=		a
	l		√41

d = a√2 d² = 2h² − 2h²cosα

	4
cosα = −
	5

jup: cosα= −0,64 .. czy taki nie powinien być wynik? podstawiamy na końcu Twoje h i d i wychodzi −0,64, a nie −0,8 d²=2a²=82a²/41 2h²=50*a²/41 82a²/41−50*a²/41=−50*a²/41 * cosα 32a²/41 * −41/50a²=cosα cosα=−0,64

dero2005: d² = 2h² − 2h²cosα (a√2)² = 2h² − 2h²cosα 2a² = 2h² − 2h²cosα |:2 a² = h² − h²cosα h²cosα = h² − a²

	h2 − a2		a2		a2
cosα =		= 1 −		= 1 −		=
	h2		h2		5   ( a)2   √41

	41a2		25		41		16
= 1 −		=		−		= −		= −0,64
	25a2		25		25		25

przepraszam, ale na końcu niepotrzebnie wyciągnąłem pierwiastek

jup: każdy ma prawo do błędu, dziękuje za rozwiązanie