wektory alfa i omega: Witam, proszę o pomoc z tym zadankiem Wektor a^−>=[3,−1,2] przedstawić w postaci sumy dwóch wektorów, z których jeden jest równoległy, a drugi prostopadły do wektora b^−>=[−1,4,5]

Trivial:

	b
all = (a∘b)
	||b||

a_⊥ = a − a_ll

alfa i omega: mógłbyś to trochę rozwinąć bo nie łapie

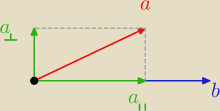Trivial: Rysunek jest w płaszczyźnie rozpiętej przez wektory a,b (przestrzeń jest n−wymiarowa). Wektor a rozkładamy na sumę dwóch wektorów: a = a_ll + a_⊥ Część a_ll jest w kierunku wektora b (a_ll = cb), a część a_⊥ jest do niego prostopadła. Bierzemy obustronnie iloczyn skalarny z b: a∘b = a_ll∘b + a_⊥∘b = cb∘b + 0 = c*||b||²

	a∘b
Skąd c =		, a zatem:
	||b||2

	a∘b
all =		b ← w poprzednim poście brakowało kwadratu przy ||b||.
	||b||2

Mając a_ll można obliczyć a_⊥: a_⊥ = a − a_ll.