pol bezendu: Obwód trapezu równoramiennego kącie ostrym 60⁰ równa się 2s (s > 0 ). Jakie powinny być wymiary tego trapezu, aby jego pole było największe? Oblicz to największe pole. a+b+2c=2s

Maslanek: Przedstaw obwód za pomocą b i c, gdzie b−krótsz apodstawa, c−ramię Jak? Wykorzystaj zależność między długościami dłuższej i krótszej podstawy oraz funkcje trygonometryczne dla obliczenia pozostałych kawałków podstawy dłuższej (if u know what i mean ) A potem pole z klasycznego wzoru

bezendu: @Maślanek Trigonometric functions? Why?

bezendu: Nie było pytania !

Maslanek: Triangle with c, h (trapezoid height) and x lengths

bezendu: Ok, ok thank you

Mila: a+b=2s−2c

	c√3
Ptrapezu=(s−c)*h, gdzie h=
	2

	s
oblicz wartość cw=
	2

1		a−b
	c=		, prosty układ i wszystko pieknie wychodzi
2		2

	3
a=		s itd
	4

bezendu: Ale znowu tyle zależności ? Gubię się w tym.

Mila: Właśnie bardzo mało.

bezendu: s, c, a,b dla mnie to już dużo i chyba za dużo.

Mila: A jak Ty rozwiązałeś ?

bezendu: Nie rozwiązałem, myślałem, że to co podał maślanek wystarczy ale coś nic z tego się nie urodziło.

Mila: Myśl, dalej. Wyjdzie. Dobranoc

bezendu: Dobranoc.

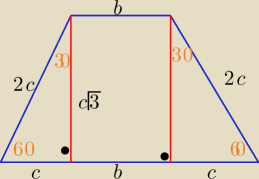
Eta: Zastosuj związki miarowe dla trójkąta 'ekierki" Ob= .... i P=....

bezendu: Obw=6c+2b=2s 2b+6c=2s/2 b+c=s

Eta: Jak to podzieliłeś? ?

bezendu: sorry b+3c=s

Eta: No Teraz pole ......

bezendu:

	a+b
P=		*h
	2

Maslanek: Wystarcza To to samo co Ety

Eta: Etam P=(b+c)*c√3 i wyznacz b z b+3c=s otrzymasz P(c)=....

bezendu: Dziękuję wrócę jutro bo dziś już nie mam siły. Dobranoc.

Eta: Miłych snów ...nie tylko o trapezach

zawodus: Widzę Eta, że lubisz trapezy Zdajesz w tym roku do drugiej klasy?

Eta: Nie wiem czy zdam

zawodus: Biedna Eta . Może jakieś korki ci załatwię

bezendu: Nie zdasz ale chyba z wf bo nie chodzisz

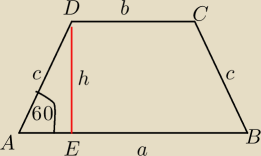
Mila: a+b+2c=2s z treści zadania

	1		a−b
|AE|=		c =		⇔c=a−b
	2		2

	c√3
h=
	2

a+b=2s−2c

	a+b
Ptrapezu=		*h⇔
	2

	(2s−2c)		c√3
Ptrapezu=		*		⇔
	2		2

	c√3		s√3		√3
Ptrapezu=(s−c)*		=c*		−c2
	2		2		2

	s
cw=
	2

	s
a+b=2s−2*		=s
	2

a−b=c⇔ a+b=s

	s
a−b=
	2

	3
a=		s
	4

	1
b=		s
	4

bezendu: Dziękuję.

Mila:

bezendu: Mila masz takie zadania jak to z matury maj 2013 R ? Nie mogę znaleźć tego typu zadań ?

Mila: Coś znajdę.O które zadania Ci chodzi?

bezendu: https://matematykaszkolna.pl/strona/3878.html

Mila: 1)Jeżeli skrócimy wysokość trapezu o polu 105 cm² o 2 cm i jednocześnie wydłużymy każdą z jego podstaw o 6 cm, to pole trapezu nie ulegnie zmianie. Wyznacz długość wysokości trapezu (przed zmianą). 2)W trójkącie ABC, w którym |AB| = |BC| połączono wierzchołek A punktem D na boku BC w ten sposób, że |AD| = |DB|. Wyznacz miary kątów trójkąta ABC jeżeli |∡CAD| = 18 ^o. 3)Wyznacz współrzędne punktu P , który dzieli odcinek o końcach A=(29,−15) i B=(45,13) w stosunku 1:3.

5-latek: DO zadania nr 3

	x1+kx2
xp=
	1+k

	y1+ky2
yp=		gdzie k oznacza stosunek podzialu
	1+k

bezendu: Po co jakieś dziwne wzory 5−latek ? i tak na maturze ich nikt nie będzie pamiętał. Wgl nawet nie potrzebne bo to geometria analityczna i mam środek odcinka AB a potem środek odcinka AS−k i po zadaniu Odp (33,−8)

bezendu:

5-latek: To nie sa jakies dziwne wzory . To sa wzory wlasnie z geometrii analitycznej .

	2
A co zrobisz jesli bedzie k=		? jak obliczysz wspolrzedne
	3

Piotr 10: Wtedy można wektorowo

bezendu: Pokombinuję rysunkiem. Bez sensu uczyć się 500 wzorów które potem zapomnę na maturze bo użyje tylko do jednego zdania. A do matury zostało około 37 dni więc wolę skupić się na planimetrii a nie na geometrii analitycznej.

5-latek: Czesc Piotr Pisze to bez zadnego podtekstu Ale bezendu nie lubi wektorow

Piotr 10: Witaj , ale tu dość prosto zastosować wektory, w geometrii analitycznej bardzo się przydają

bezendu: Koniec tej dyskusji, zadanie zrobione to teraz czy rysunek do zadania 2 jest dobry.

5-latek: Piotr ja o tym wiem ale bezendu kombinowal zawsze jak zrobic bez wektorow jesli mu sie to udaje to dobrze Zycze mu zeby trafil na maturze na zadanie gdzie nie bedzie potrzeby korzystania z wektorow

Piotr 10: Rysunek ok

bezendu: 5−latek na każdej maturze której robiłem nie musiałem używać wektorów zadania jest tak skonstruowane, że można je zrobić na kilka sposobów.

bezendu: To wychodzi, że 66,66 i 48 ?

Piotr 10:

bezendu: Teraz to pierwsze najtrudniejsze chyba.

bezendu: ?

Mila: Zadanie 3− dobrze. Zadanie 2 dobrze. Zadanie 1) Napisz wzór na pole trapezu na dwa sposoby Na początku:

a+b
	*h=105
2

oblicz z tego (a+b) i wstaw do drugiego równania na pole trapezu po zmianie.

bezendu: (a+b)h=210

	210
a+b=
	h

a+b+12
	*(h−2)=105
2

(a+b+12)(h−2)=210

	210
(		+12)(h−2)=210
	h

	420
210−		+12h−24−210=0
	h

takie coś ?

Mila: Bardzo dobrze. Pisz dalej, bo chcę wiedzieć jak to rozwiązujesz.

bezendu:

	420
−		+12h−24=0 /h
	h

−420+12h²−24h=0 / :12 h²−2h−35=0 Δ=144 √Δ=12 h=7

Mila: W porządku. h=−5 nie odpowiada warunkom zadania, h>0.

bezendu: Tak wiem, dlatego napisałem tylko wynik dodatni.

bezendu: A co myślisz o tym co napisał Godzio ?

Mila: Każdy musi sam znaleźć swoją ścieżkę do wiedzy. Godzio napisał, to co sama bym Ci doradziła. Najpierw co widzę na rysunku, co umiem obliczyć, co mogę obliczyć , zadajesz sobie pytania i próbujesz rozwiązać problem. Czasem bardzo długo myślałam nad zadaniem, podejmowałam różne próby, w końcu gdy rozwiązałam, to zapamiętałam sposób i popełniane błędy. Na studia masz się dostać i utrzymać. To drugie jest trudniejsze. Pracujesz dużo i coraz lepiej Ci wychodzi. Niektóre zadania bardzo ładnie rozwiązujesz , są takie co dalej sprawiają Ci duży kłopot. Pracuj dalej, po maturze też.

bezendu: I właśnie na miesiąc przed maturą chce Jeszce bardziej pracować nad planimetria i brylami

Mila: 1) Rysunek przedstawia kształt obszaru zakreślanego przez wycieraczkę samochodową. Wiedząc, że ∡AOC=150^o oraz |AB|=|BO oblicz jakie jest pole obszaru oczyszczanego przez wycieraczkę. Przyjmując, że π≈3,14

Mila: Dobranoc

bezendu: Czyli trzeba policzyć cały obszar −mały obszar nie zakreślony przez wycieraczki ?

bezendu: ?

zawodus: a jak sobie to inaczej wyobrażasz?

bezendu: AB=x BO=x

	150
P1=		*3,14*(2x)2
	360

	157
P1=		4x2
	120

	157
P2=		x2
	120

	157x2		157x2		157
Pobszaru=P1−P2=		−		=		x2
	30		120		40

bezendu: ?

Mila:

	150		15		5
Dlaczego nie uprościłeś?		=		=
	360		36		12

|AB|=|BO|=0,3m Podstaw i dokończ

bezendu: P_o=0,35 m

Mila: w zaokrągleniu ≈

bezendu: A no tak dziękuję za uwagę.